两个有序数组的中位数

背景

给定两个大小分别为 m 和 n 的正序（从小到大）数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。

示例 1:

输入：nums1 = [1,3], nums2 = [2]
输出：2.00000
解释：合并数组 = [1,2,3] ，中位数 2

示例 2：

输入：nums1 = [1,2], nums2 = [3,4]
输出：2.50000
解释：合并数组 = [1,2,3,4] ，中位数 (2 + 3) / 2 = 2.5

示例 3：

输入：nums1 = [0,0], nums2 = [0,0]
输出：0.00000

示例 4：

输入：nums1 = [], nums2 = [1]
输出：1.00000

示例 5：

输入：nums1 = [2], nums2 = []
输出：2.00000

首先回顾一下中位数的定义：

中位数（Median）又称中值，统计学中的专有名词，是按顺序排列的一组数据中居于中间位置的数，代表一个样本、种群或概率分布中的一个数值，其可将数值集合划分为相等的上下两部分。对于有限的数集，可以通过把所有观察值高低排序后找出正中间的一个作为中位数。如果观察值有偶数个，通常取最中间的两个数值的平均数作为中位数。

解法一

直接求中位数可能不好想到，那么我们换个思路
假设有下面两个数组 A 和 B，
A数组的长度是4，B数组的长度是8

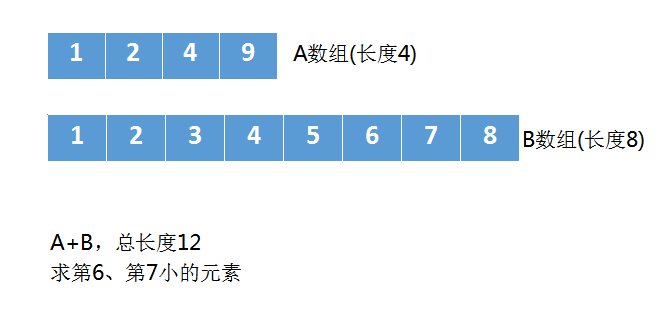
如上图，因为A+B的总长度是12，是偶数，所以求中位数的话，需要找到第6小、第7小的元素，找到这两个元素后，相加再 / 2.0就可以了。
这里是偶数长度的情况，如果是两个数组长度相加后是奇数也是类似的，比如总长度是 13 ，那就需要找第7小的元素。

所以，这题可以转化为，如何找到第k小的元素。

如果总长度N是偶数，则需要找到两个数组中第N / 2小的元素、第N / 2 + 1小的元素
如果总长度N是奇数，则需要找到两个数组中第N / 2 + 1小的元素

题目限制了时间复杂度，所以这里找第k小的过程，肯定也是二分的方式。
因为数组A、数组B都是有序的，所以我们需要利用这个有用的特性，每次缩小查找范围
第一次找 k 小、第二次就是找 k/2 小、然后是 k/4小，直到 k 等于1时。

还是以上面的数组为例，A数组为[1,2,4,9]，B数组是[1,2,3,4,5,6,7,8]
我们需要找第6、第7小的元素，假设我们先找第6小的元素，也就是k = 6。我们首先比较 A数组中第3个元素，B数组中第3个元素，也就是A[k/2-1]和B[k/2-1]，如下图：

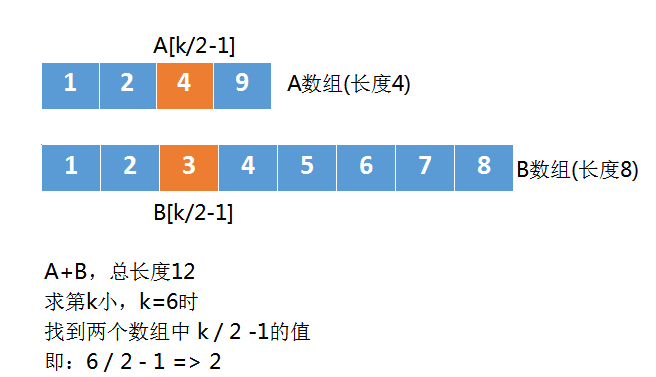
由于A[k/2-1] > B[k/2-1]，这时候我们就可以忽略掉一些元素了。
上图中 A数组中的4，它前面有2个元素，也就是k/2-1个元素，B数组的3，它前面也有2个元素，也就是k/2-1个元素，所以橙色的4和3前面一共有k-2个元素。

假设 B数组的3，也就是B[k/2-1] 比这k-2个元素都大。
而 B[k/2-1] 是小于 A[k/2-1]的，那么B[k/2-1]相当于是第k-1小的，所以，第k小的元素肯定不是它。
这样的话，我们就可以排除一些元素了，刚才我们只是假设B[k/2-1] 比 A[k/2-1]前面的元素大，实际可能不是。
但有一点可以肯定，既然B[k/2-1]都不是第k小的元素，那么 B[k/2-1]前面的那些更不是了，于是我们将B[0]、B[1]、B[2]。。。B[k/2-1]这些元素全部忽略掉。

当我们忽略掉 B数组中的元素后， k也要跟着减小，原来我们求第6小，现在就是求第3小。
这个解法的整体求解过程，就是不断缩小数组的规模，同时把k也跟着缩小。如下图

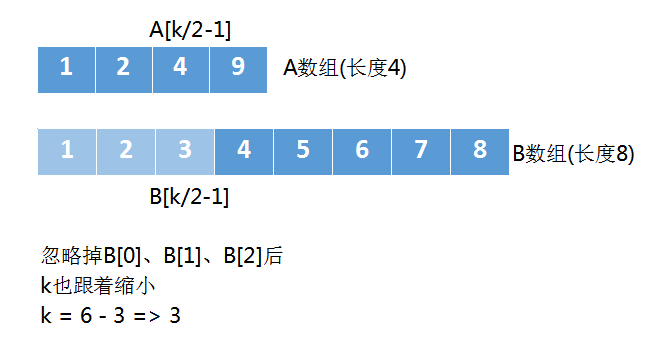
这次 k=3，k/2-1=>0
所以A[k/2-1]对应的就是A[0]
B[k/2-1]对应是B[3]，因为我们之前忽略掉了 B数组中的前3个元素，所以B数组的第1个元素是从下标3开始的。如下图：

经过这次比较后，A[k/2-1] < B[k/2-1]，所以忽略掉A[0]，然后将 k 变成2。

k此时等于2，k/2-1=>0
于是A[k/2-1]对应的是A[1]，因为刚才已经忽略掉A[0]了
B[k/2-1]对应的是B[3]
如下图：

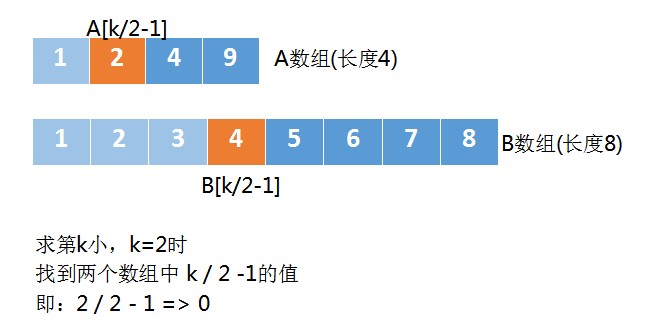
当k==1时，返回A数组中第一个元素和 B数组中第一个元素的较小者。
此时A数组中的第1个元素是A[2]，B数组中第1个元素是B[3]，即求min(A[2],B[3])

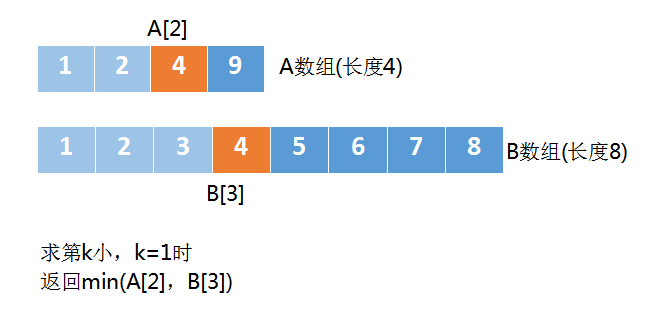
还有一些特殊情况，A数组长度为2，B数组长度为10，求第6小时，A数组计算得到A[k/2-1]是A[2]越界了，对于这种情况，我们就拿 A数组中最后一个元素即可。

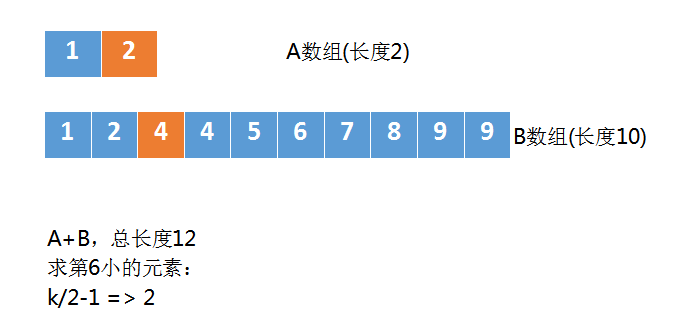
总结一下，对于求第k小的元素，其过程如下：

如果A[k/2-1] <= B[k/2-1]，将A[0] - A[k/2-1]这些元素全部忽略掉
否则，将B[0] - B[k/2-1] 这些元素全部忽略掉

时间复杂度：$O(log(m+n))$，初始化长度为m+n，每次查询都会减半
空间复杂度：$O(1)$

代码实现：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47


class Solution(object):
    def findMedianSortedArrays(self, nums1, nums2):
        total = len(nums1) + len(nums2)
        # 如果A数组长度+B数组长度total是奇数，则找total/2+1小的元素
        # 即为中位数
        if total % 2 == 1:
            midIndex = total / 2 + 1
            res = self.getKthElement(nums1, nums2, midIndex)
            return float(res)
        # 否则，找total/2，total/2+1这两个元素    
        else:
            midIndex_1 = total / 2
            midIndex_2 = total / 2 + 1
            a = self.getKthElement(nums1, nums2, midIndex_1)
            b = self.getKthElement(nums1, nums2, midIndex_2)
            return (a + b) / 2.0

    def getKthElement(self,nums1, nums2, k):
        len1 = len(nums1)
        len2 = len(nums2)
        index1 = 0
        index2 = 0
        while True:
            # 边界情况，当index1越界时，直接返回nums2的第k小元素
            if index1 == len1:
                return nums2[index2 + k -1]
            # 边界情况，当index2越界时，直接返回nums1的第k小元素
            if index2 == len2:
                return nums1[index1 + k - 1]
            # 边界情况，k等于1时，返回nums1第一个元素和nums2第一个元素较小者
            if k == 1:
                return min(nums1[index1], nums2[index2])
            new_index1 = min(index1 + k / 2, len1) - 1 
            new_index2 = min(index2 + k / 2, len2) - 1
            pivot1 = nums1[new_index1]
            pivot2 = nums2[new_index2]
            # 比较nums1[k/2-1]和nums2[k/2-1]
            # 如果nums1的小，则忽略掉nums1[0] - nums1[k/2-1]这些元素
            # 再更新 k，k 要减去忽略掉的那些元素，index1也要更新，待下轮使用
            if pivot1 <= pivot2:
                k -= (new_index1 - index1 + 1)
                index1 = new_index1 + 1
            # 如果nums2的小，则忽略掉nums2[0] - nums2[k/2-1]这些元素
            # 再更新 k，k 要减去忽略掉的那些元素，index2也要更新，待下轮使用
            else:
                k -= (new_index2 - index2 + 1)
                index2 = new_index2 + 1

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59


class Solution {
    public double findMedianSortedArrays(int[] nums1, int[] nums2) {
        int len1 = nums1.length;
        int len2 = nums2.length;
        int total = len1 + len2;
        //如果A数组长度+B数组长度total是奇数，则找total/2+1小的元素即为中位数
        if(total % 2 == 1) {
            int midIndex = total / 2 + 1;
            return getKthElement(nums1, nums2, midIndex);
        }
        //否则，找total/2，total/2+1这两个元素  
        else {
            int midIndex_1 = total / 2;
            int midIndex_2 = total / 2 + 1;
            double a = getKthElement(nums1, nums2, midIndex_1);
            double b = getKthElement(nums1, nums2, midIndex_2);
            return (a + b) / 2.0D;
        }
    }
    
    private int getKthElement(int[] nums1, int[] nums2, int k) {
        int len1 = nums1.length;
        int len2 = nums2.length;
        int index1 = 0;
        int index2 = 0;
        while(true) {
            //边界情况，当index1越界时，直接返回nums2的第k小元素
            if(index1 == len1) {
                return nums2[index2 + k - 1];
            }
            //边界情况，当index2越界时，直接返回nums1的第k小元素
            if(index2 == len2) {
                return nums1[index1 + k - 1];
            }
            //边界情况，k等于1时，返回nums1第一个元素和nums2第一个元素较小者
            if(k == 1) {
                return Math.min(nums1[index1], nums2[index2]);
            }
            int half = k / 2;
            int newIndex1 = Math.min(index1 + half, len1) - 1;
            int newIndex2 = Math.min(index2 + half, len2) - 1;
            int pivot1 = nums1[newIndex1];
            int pivot2 = nums2[newIndex2];
            //比较nums1[k/2-1]和nums2[k/2-1]
            //如果nums1的小，则忽略掉nums1[0] - nums1[k/2-1]这些元素
            //再更新 k，k 要减去忽略掉的那些元素，index1也要更新，待下轮使用
            if(pivot1 <= pivot2) {
                k -= (newIndex1 - index1 + 1);
                index1 = newIndex1 + 1;
            }
            //如果nums2的小，则忽略掉nums2[0] - nums2[k/2-1]这些元素
            //再更新 k，k 要减去忽略掉的那些元素，index2也要更新，待下轮使用
            else {
                k -= (newIndex2 - index2 + 1);
                index2 = newIndex2 + 1;
            }
        }
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62


object Solution {
    def findMedianSortedArrays(nums1: Array[Int], nums2: Array[Int]): Double = {
        var len1 = nums1.length
        var len2 = nums2.length
        var total = len1 + len2
        //如果A数组长度+B数组长度total是奇数，则找total/2+1小的元素即为中位数
        if(total % 2 == 1) {
            var midIndex = total / 2 + 1
            var res = getKElement(nums1, nums2, midIndex)
            return res.toDouble
        }
        //否则，找total/2，total/2+1这两个元素  
        else {
            var midIndex_1 = total / 2
            var midIndex_2 = total / 2 + 1
            var a = getKElement(nums1, nums2, midIndex_1)
            var b = getKElement(nums1, nums2, midIndex_2)
            return (a + b) / 2.0
        }
    }

    def getKElement(nums1: Array[Int], nums2: Array[Int], _k: Int): Int = {
        var len1 = nums1.length
        var len2 = nums2.length
        var index1 = 0
        var index2 = 0
        var k = _k
        while(true) {
            //边界情况，当index2越界时，直接返回nums1的第k小元素
            if(index1 == len1) {
                return nums2(index2 + k - 1)
            }
            //边界情况，当index2越界时，直接返回nums1的第k小元素
            if(index2 == len2) {
                return nums1(index1 + k - 1)
            }
            //边界情况，k等于1时，返回nums1第一个元素和nums2第一个元素较小者
            if(k == 1) {
                return Math.min(nums1(index1), nums2(index2))
            }
            var half = k / 2
            var newIndex1 = Math.min(index1 + half, len1) - 1
            var newIndex2 = Math.min(index2 + half, len2) - 1
            var pivot1 = nums1(newIndex1)
            var pivot2 = nums2(newIndex2)
            //比较nums1[k/2-1]和nums2[k/2-1]
            //如果nums1的小，则忽略掉nums1[0] - nums1[k/2-1]这些元素
            //再更新 k，k 要减去忽略掉的那些元素，index1也要更新，待下轮使用
            if(pivot1 <= pivot2) {
                k -= (newIndex1 - index1 +1)
                index1 = newIndex1 + 1
            }
            //如果nums2的小，则忽略掉nums2[0] - nums2[k/2-1]这些元素
            //再更新 k，k 要减去忽略掉的那些元素，index2也要更新，待下轮使用
            else {
                k -= (newIndex2 - index2 + 1)
                index2 = newIndex2 + 1
            }
        }
        return -1
    }
}

解法二

我们通过数组切分的方式来求中位数，先看看怎么个切法。
我们把 A、B 两个数组排好，然后一刀切。把 A数组分为两半， B数组也分为两半。如下图：

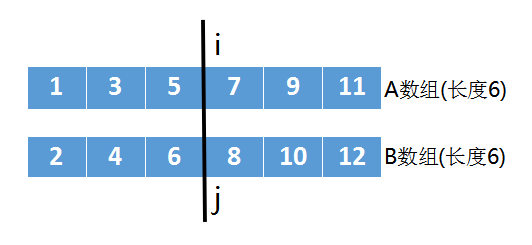
我们把 i的左边和j的左边统称为 左半部分
把i的右边和j的右边统称为右半部分
上图中，经过切割后，左半部分的任意值都小于 右半部分。

当A、B两个数组总长度为偶数时，左半部分的长度等于右半部分的长度
假设A数组长度为m， B数组长度为n，可得下面等式：

左半部分 = m - i + n - j
右半部分 = i + j
m - i + n - j == i + j

当两个数组总长度为偶数时，我们取左半部分的最大值、右半部分的最小值，把这两个值相加再/2.0就可以得到中位数了，如下图：

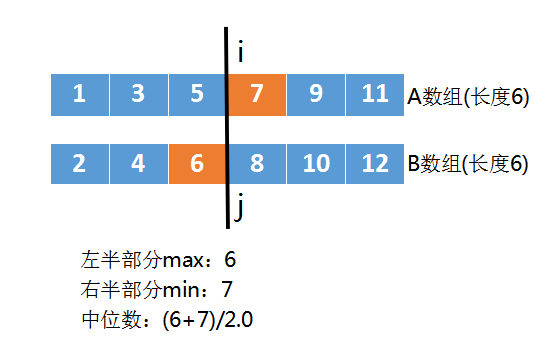
刚才我们讨论的都是两数组长度为偶数的情况，如果两个数组长度为奇数呢？
长度为奇数时，左半部分必定和右半部分长度不等，我们令左半部分长度 = 右半部分长度 + 1
这样中位数就是左半部分的最大值，如下图：

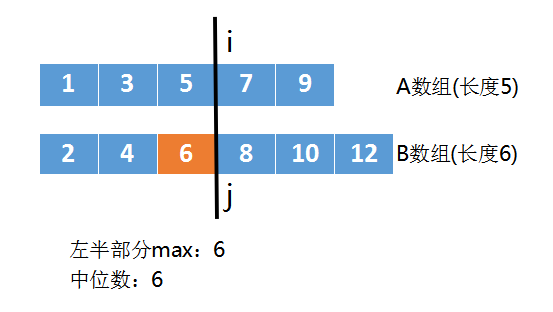
于是我们可以得到下面等式(假设A数组长度为m，B数组长度为n)：

左半部分 = m - i + n - j + 1
右半部分 = i + j
m - i + n - j + 1 = i + j

怎么求i和j呢？
因为题目限制了时间，所以求 i 和 j 肯定也是基于二分查找。
i的求法很简单，就是基于二分查找即可，拿到A数组的 begin 和 end，即可求出 i。
j的求法就麻烦很多了，但刚才我们已经发现这么一个等式：

两数组总长度为偶数时：m - i + n - j == i + j
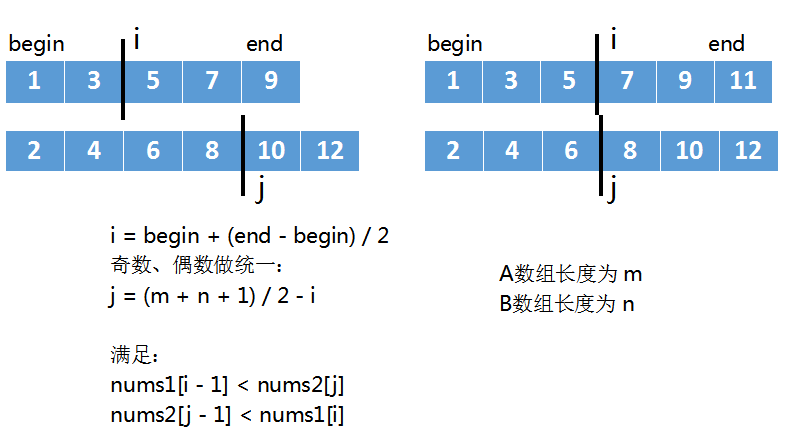
两数组总长度为奇数时：m - i + n - j + 1 == i + j 我们可以把奇数长度、偶数长度做个统一，根据上面两个公式计算出j：

j = (m + n + 1) / 2 - i

i 和 j 切分后，会得到左半部分、右半部分，左半部分的最大值，是小于右半部分最小值的，即：

nums1[i - 1] < nums2[j]
nums2[j - 1] < nums1[i]

如下图所示：

如果不满足两个条件，说明切的位置不对，我们就要调整切分的位置。
调整的方式当时也是基于二分的，

如果i的值取大了，会出现 nums1[i - 1] > nums2[j]，让 end = i - 1
如果i的值取小了，会出现 nums1[i] < nums2[j - 1]，让 begin = i + 1

因为j是等于(m + n + 1) / 2 - i，当我们调整了i，j也会跟着调整。
我们通过二分的方式调整i和j就可以找到对应的中位数了。

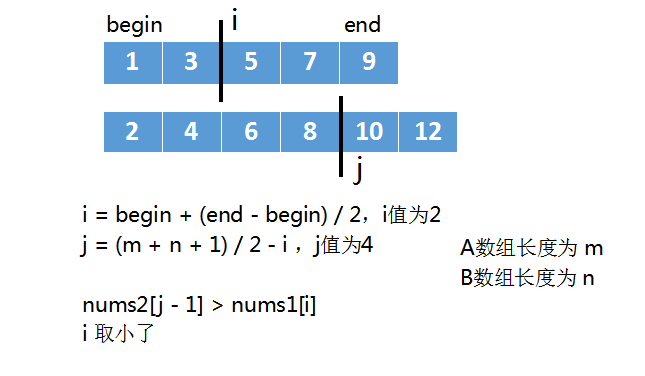
我们以A数组[1,3,5,7,9]，B数组[2,4,6,8,10,12]为例，看看查找中位数的过程。
首先计算出i和j，i为2，j为4。
nums2[j - 1] > nums1[i]，此时说明i的值取小了，如下图：

我们调整i，令 begin = i + 1，计算i和j。
这次发现 nums1[i - 1] > nums2[j]，也就是i的值取大了，如下图：

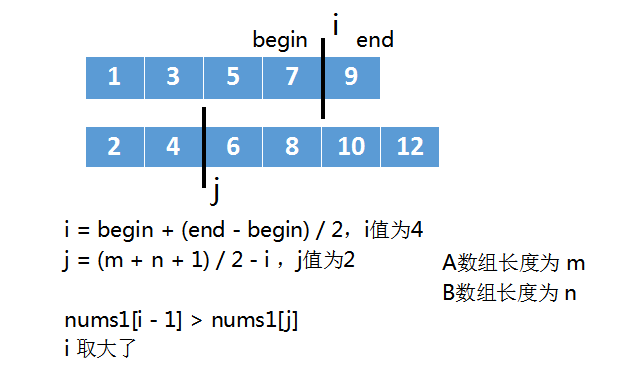
再次调整i，令end = i - 1，并再次计算i和j。
这回终于满足条件了：

nums1[i - 1] < nums2[j]
nums2[j - 1] < nums1[i]

中位数为： max(nums1[i - 1], nums2[j - 1])，也就是6，如下图：

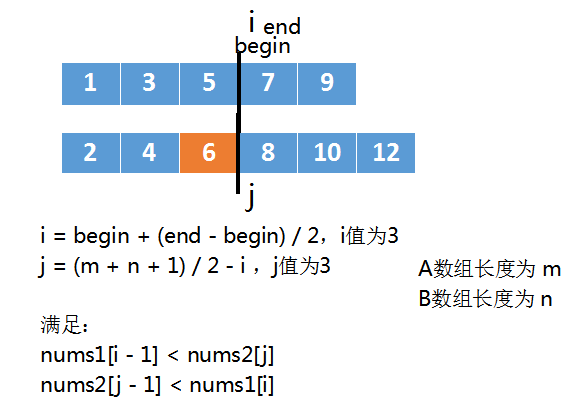
还有一些特殊情况我们需要处理一下，当 i == 0时，说明 A数组切分后左半部分是空的。
此时左半部分的最大值就是nums2[j - 1]。
同理，如果j == 0，说明 B数组切分后左半部分是空的。
此时左半部分的最大值就是nums1[i - 1]
如下图：

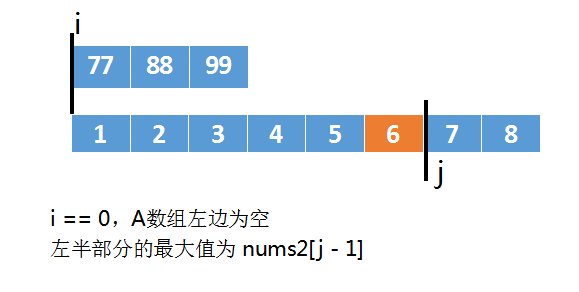
当i == m时，说明 A数组切分后右半部分是空的。此时右半部分的最小值就是nums2[j]。
同理，如果j == n，说明 B数组切分后右半分是空的。
此时右半部分的最小值就是nums1[i]。

时间复杂度：$O(log_{min(m,n)})$，其中 m 和 n 分别是nums1和nums2的长度，我们基于长度较短的数组做切分min(m,n)，每次切分后都会将查找规模减半，因此总时间是对数级别的。
空间复杂度：$O(1)$

代码实现：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67


class Solution {
    public double findMedianSortedArrays(int[] nums1, int[] nums2) {
    	if(nums1.length > nums2.length) {
            return findMedianSortedArrays(nums2, nums1);
        }
        int m = nums1.length;
        int n = nums2.length;
        int begin = 0;
        int end = m;
        //左半部分的最大值
        double left_max = Double.MIN_VALUE;
        //右半部分的最小值
        double right_min = Double.MAX_VALUE;
        while(begin <= end) {
            //基于二分的方式求 i
            int i = begin + (end - begin) / 2;
            //数组A长度为m，数组B长度n，总长度为偶数时，左半部分右半部分相等：
            //m - i + n - j = i + j
            //总长度为奇数时，左半部分比右半部分多1个：
            //m - i + n - j + 1 = i + j
            //统一奇数、偶数情况，得到j为：(m + n + 1) / 2 - i
            int j = (m + n + 1) / 2 - i;
            //如果nums1[i - 1] > nums2[j]说明 i 取大了
            if(i > 0 && j < n && nums1[i - 1] > nums2[j]) {
                end = i - 1;
            }
            //nums2[j - 1] > nums1[i]，i 取小了
            else if(j > 0 && i < m && nums2[j - 1] > nums1[i]) {
                begin = i + 1;
            }
            //满足条件：nums1[i - 1] < nums2[j]，nums2[j - 1] < nums1[i]
            else {
                //边界情况，数组A切分后左半部分为空 i == 0
                //数组B 切分后左半部分为空 j == 0
                if(i == 0) {
                    left_max = nums2[j - 1];
                }
                else if(j == 0) {
                    left_max = nums1[i - 1];
                }
                //求左半部分的最大值
                else {
                    left_max = Math.max(nums1[i - 1], nums2[j - 1]);
                }
                //总长度为奇数时，直接返回左半部分最大值即可
                if((m + n) % 2 == 1) {
                    return left_max / 1.0;
                }
                //边界情况，数组A 切分后，右半部分为空 i == m
                //数组B 切分后，右半部分为空 j == n
                if(i == m) {
                    right_min = nums2[j];
                }
                else if(j == n) {
                    right_min = nums1[i];
                }
                //求右半部分的最小值
                else {
                    right_min = Math.min(nums1[i], nums2[j]);
                }
                //总长度为偶数时
                return (left_max + right_min) / 2.0;
            }
        }
        return 0.0D;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53


class Solution(object):
    def findMedianSortedArrays(self, nums1, nums2):
        if len(nums1) > len(nums2):
            return self.findMedianSortedArrays(nums2,nums1)
        m = len(nums1)
        n = len(nums2)
        begin = 0
        end = m
        # 左半部分的最大值
        left_max = float("-inf")
        # 右半部分的最小值
        right_min = float("inf")
        while begin <= end:
            # 基于二分的方式求 i
            i = begin + (end - begin) // 2 
            # 数组A长度为m，数组B长度n，总长度为偶数时，左半部分右半部分相等：
            # m - i + n - j = i + j
            # 总长度为奇数时，左半部分比右半部分多1个：
            # m - i + n - j + 1 = i + j
            # 统一奇数、偶数情况，得到j为：(m + n + 1) / 2 - i
            j = (n + m + 1) // 2 - i
            # 如果nums1[i - 1] > nums2[j]说明 i 取大了
            if i > 0 and j < n and nums1[i - 1]>nums2[j]:
                end = i - 1
            # nums2[j - 1] > nums1[i]，i 取小了    
            elif j > 0 and i < m and nums2[j - 1]>nums1[i]:
                begin = i + 1
            #满足条件：nums1[i - 1] < nums2[j]，nums2[j - 1] < nums1[i]    
            else:
                # 边界情况，数组A切分后左半部分为空 i == 0
                # 数组B 切分后左半部分为空 j == 0
                if i == 0:
                    left_max = nums2[j - 1]
                elif j == 0:
                    left_max = nums1[i - 1]
                # 求左半部分的最大值    
                else:
                    left_max = max(nums1[i - 1],nums2[j - 1])
                # 总长度为奇数时，直接返回左半部分最大值即可    
                if (n + m) % 2 == 1:
                    return float(left_max)
                # 边界情况，数组A 切分后，右半部分为空 i == m
                # 数组B 切分后，右半部分为空 j == n
                if i == m:
                    right_min = nums2[j]
                elif j == n:
                    right_min = nums1[i]
                # 求右半部分的最小值    
                else:
                    right_min = min(nums1[i],nums2[j])
                # 总长度为偶数时    
                return (left_max + right_min) / 2.0
        return 0.0

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67


object Solution {
    def findMedianSortedArrays(nums1: Array[Int], nums2: Array[Int]): Double = {
        if(nums1.length > nums2.length) {
            return findMedianSortedArrays(nums2, nums1)
        }
        var m = nums1.length
        var n = nums2.length
        var begin = 0
        var end = m
        //左半部分的最大值
        var left_max = -9999999999.0
        //右半部分的最小值
        var right_min = 9999999999.0
        while(begin <= end) {
            //基于二分的方式求 i
            var i = begin + (end - begin) / 2
            //数组A长度为m，数组B长度n，总长度为偶数时，左半部分右半部分相等：
            //m - i + n - j = i + j
            //总长度为奇数时，左半部分比右半部分多1个：
            //m - i + n - j + 1 = i + j
            //统一奇数、偶数情况，得到j为：(m + n + 1) / 2 - i
            var j = (n + m + 1) / 2 - i
            //如果nums1[i - 1] > nums2[j]说明 i 取大了
            if(i > 0 && j < n && nums1(i - 1) > nums2(j)) {
                end = i - 1
            }
            //nums2[j - 1] > nums1[i]，i 取小了
            else if(j > 0 && i < m && nums2(j - 1) > nums1(i)) {
                begin = i + 1
            }
            //满足条件：nums1[i - 1] < nums2[j]，nums2[j - 1] < nums1[i]
            else {
                //边界情况，数组A切分后左半部分为空 i == 0
                //数组B 切分后左半部分为空 j == 0
                if(i == 0) {
                    left_max = nums2(j - 1)
                }
                else if(j == 0) {
                    left_max = nums1(i - 1)
                }
                //求左半部分的最大值
                else {
                    left_max = Math.max(nums1(i - 1), nums2(j - 1))
                }
                //总长度为奇数时，直接返回左半部分最大值即可
                if((n + m) % 2 == 1) {
                    return left_max / 1.0
                }
                //边界情况，数组A 切分后，右半部分为空 i == m
                //数组B 切分后，右半部分为空 j == n
                if(i == m) {
                    right_min = nums2(j)
                }
                else if(j == n) {
                    right_min = nums1(i)
                }
                //求右半部分的最小值
                else {
                    right_min = Math.min(nums1(i), nums2(j))
                }
                //总长度为偶数时
                return (left_max + right_min) / 2.0
            }
        }
        return 0.0
    }
}

背景

解法一

解法二

最近文章

分类

归档

标签

RSS