背景
二叉树的遍历有三种,前序、中序、后序。
这三种遍历用递归实现非常简单:
- 前序遍历:打印根节点、遍历左子树、遍历右子树
- 中序遍历:遍历左子树、打印根节点、遍历右子树
- 后序遍历:遍历左子树、遍历右子树、打印根节点
递归版本很简单,用栈模拟递归也不难,本文主要说说莫里斯遍历,顺带补充迭代版本。
莫里斯遍历是由 J. H. Morris 在 1979 年的论文「Traversing Binary Trees Simply and Cheaply」中首次提出,因此被称为 Morris 遍历。
Morris 遍历的核心是利用树中的空闲指针,将空间缩减为常数。
前序、中序、后序遍历的时间复杂度都是 $O(N)$
前序、中序、后序遍历的递归和栈模拟递归版本 空间复杂度是 $O(h)$,这里的h是树的高度。
前序、中序、后续遍历的莫里斯版本空间复杂度是 $O(1)$
前序遍历
迭代版本
这里就是模拟递归调用:
打印根节点
dfs(root.left)
打印根节点
dfs(root.left)
root为空返回
dfs(root.right)
dfs(root.left)
dfs(root.right)
dfs(root.right)
打印根节点
dfs(root.left)
dfs(root.right)
也就是先打印根节点、再一直遍历左节点(入栈),如果左边为空则则出栈,遍历右节点。
Python代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
class Solution(object):
def preorderTraversal(self, root):
res = []
stack = []
while root or stack:
# 不断往左子树方向走,每走一次就将当前节点保存到栈中
# 这是模拟递归的调用
if root:
res.append(root.val)
stack.append(root)
root = root.left
# 当前节点为空,说明左边走到头了,从栈中弹出节点并保存
# 然后转向右边节点,继续上面整个过程
else:
tmp = stack.pop()
root = tmp.right
return res
|
莫里斯遍历-1
这是破坏性的版本,传入的是一颗二叉树,等遍历完后,这棵二叉树就变成链表了。
它的原理是改变二叉树的结构,让根节点的左子树的最右节点 -指向-> 根节点的右子树,再把根节点的左子树变成右子树,伪代码如下:
root.left.最右节点.right = root.right
root.right = root.left
root.left = None
图解如下,第一步,把5(根节点的左子树的最右节点),指向3(根节点的右节点),再把跟节点的左子树变成右子树:
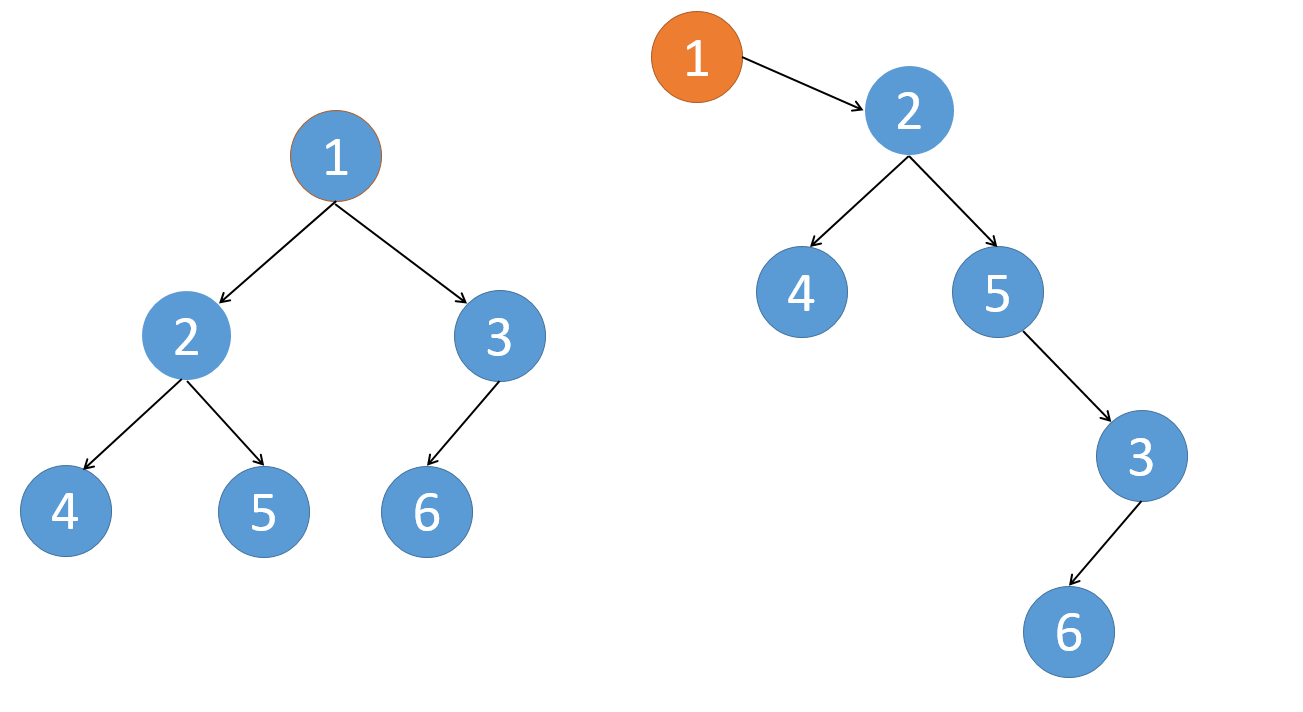
之后,用root.right挨个遍历就可以了,直到3这个节点时,将其子节点6调整到右边。
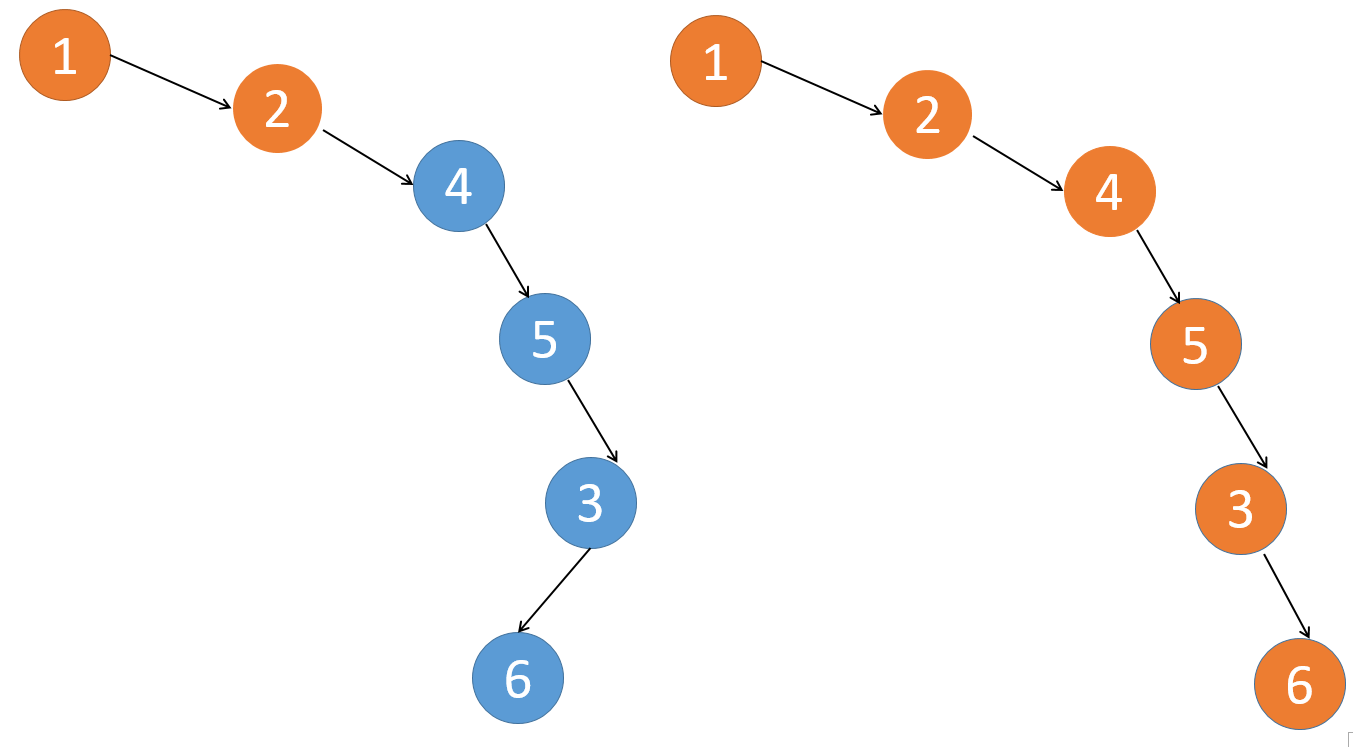
代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
|
class Solution(object):
def preorderTraversal(self, root):
res = []
while root:
if root.left:
# 如果左子树不空,则找到左子树的最右节点
pre = root.left
while pre.right:
pre = pre.right
# 将左子树最右节点.right 指向根节点的右子树
pre.right = root.right
# 将左子树调整为右子树,并将左边置为空
root.right = root.left
root.left = None
else:
# 此时树就变成链表了,不断访问右节点即可
res.append(root.val)
root = root.right
return res
|
莫里斯遍历-2
这里使用了空闲指针的方式,同样也是找到 根节点左子树的最右节点,让其指向 根节点,然后根节点继续往左遍历。
root.left.最右节点.right = root
root = root.left
对应到下图,让5的right指向1,再让4的right指向2。
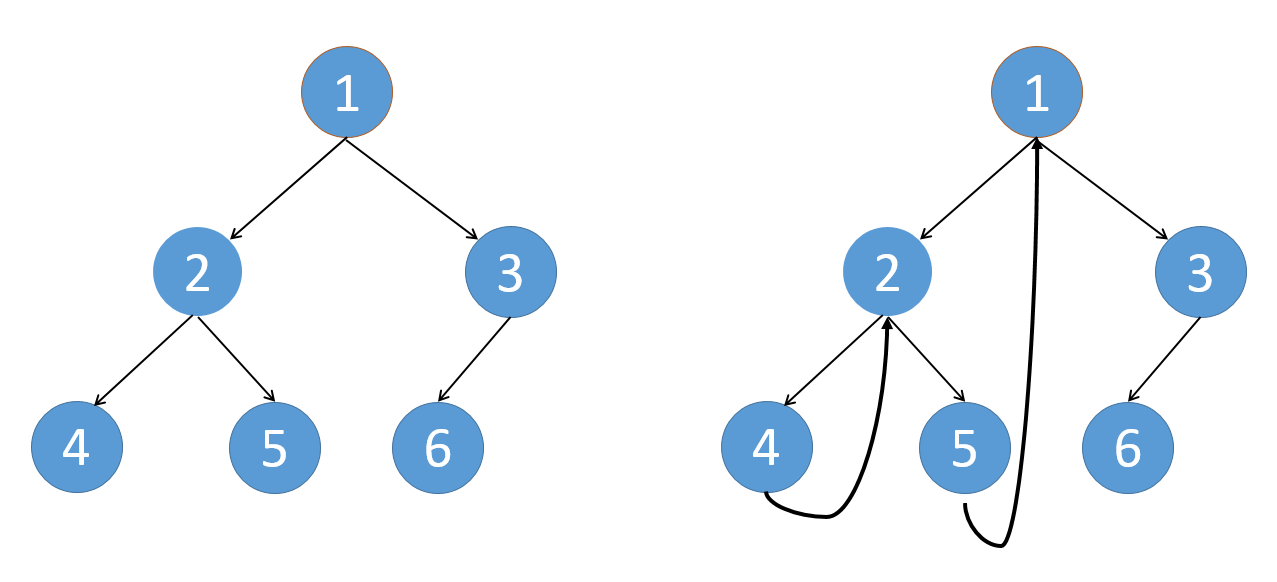
当左边遍历完后,就往右遍历,由于4的右边是2。当我们再次访问到2时,发现2的左子树最右节点4的right等于2。
这就说明2是被访问过了,所以就可以断开4的right,让其指向空,恢复二叉树的结构,同时让2继续往右走。
对于1也是一样,当再次遍历到1时,就可以断开5的right了。
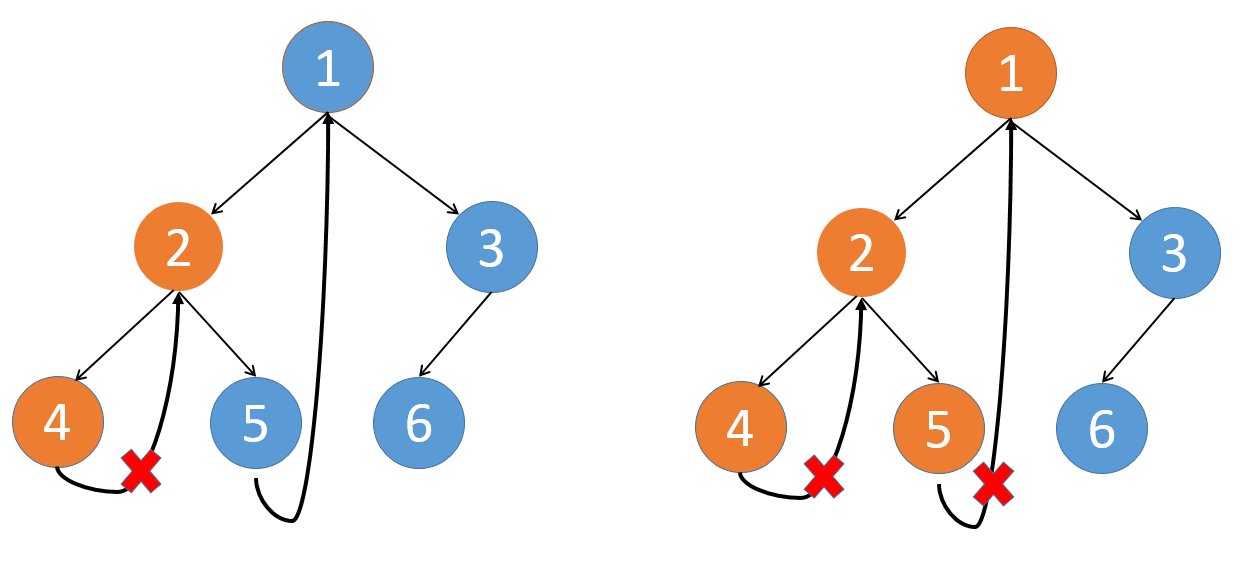
Python代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
|
class Solution(object):
def preorderTraversal(self, root):
res = []
while root:
if root.left:
# 找到根节点左子树的最右节点
tmp = root.left
while tmp.right and tmp.right != root:
tmp = tmp.right
# 如果最右节点.right不为空,说明是第一次访问
if not tmp.right:
# 第一次访问,加入到结果集中
res.append(root.val)
# 并将右节点指向根
tmp.right = root
# 根节点继续往左访问
root = root.left
# 最右节点不空,说明访问过了,要断开
else:
tmp.right = None
root = root.right
# 访问根的右边
else:
res.append(root.val)
root = root.right
return res
|
中序遍历
迭代版本
Python代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
class Solution(object):
def inorderTraversal(self, root):
res = []
stack = []
while root or stack:
# 不断往左子树方向走,每走一次就将当前节点保存到栈中
# 这是模拟递归的调用
if root:
stack.append(root)
root = root.left
# 当前节点为空,说明左边走到头了,从栈中弹出节点并保存
# 然后转向右边节点,继续上面整个过程
else:
node = stack.pop()
res.append(node.val)
root = node.right
return res
|
莫里斯遍历-1
中序遍历的破坏版本,跟前序遍历很类似。前序遍历是先打印跟、再遍历左、再是右。所以改变完后的树结构是:
root.left.最右节点.right = root.right
root.right -> root.left
root.left = None
对于中序遍历改造后的结构是:
root.left.最右节点.right = root
tmp = root
root = root.left
tmp.left = None
如下图,这会我们要让5的right指向1,而1的右边不动,之后把1的左边置为空。
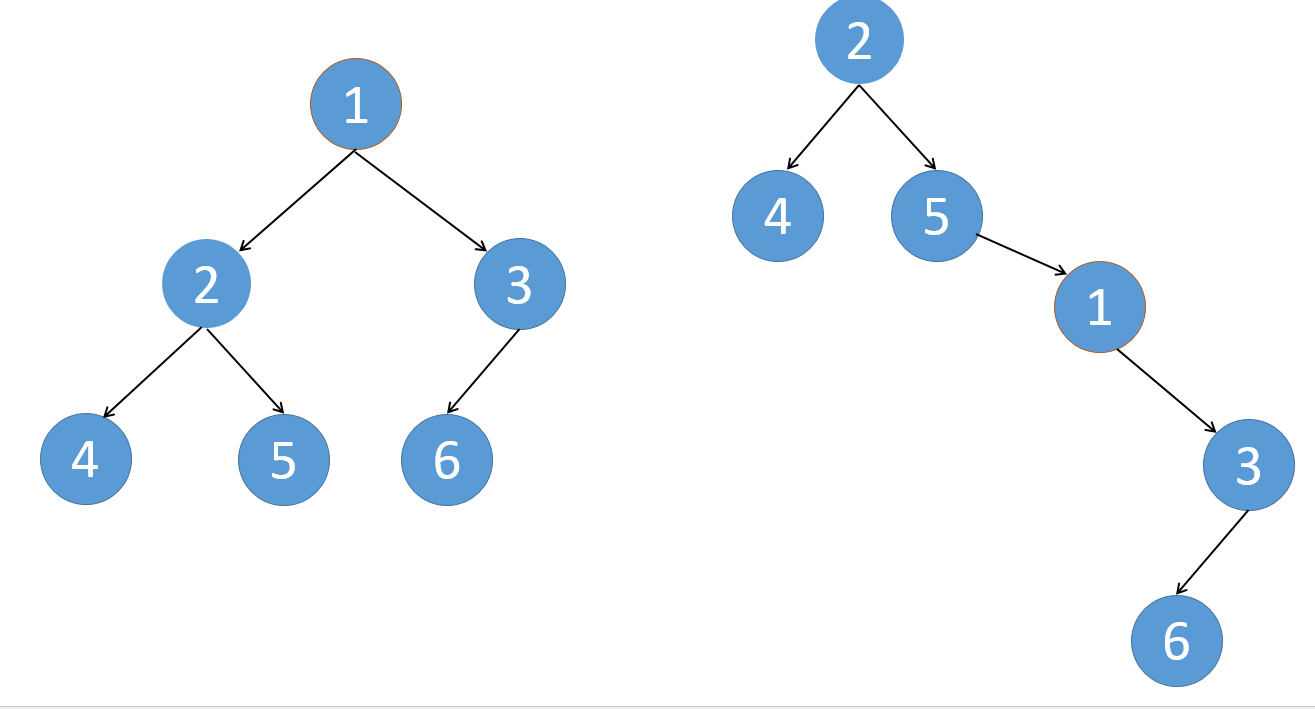
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
class Solution(object):
def inorderTraversal(self, root):
res = []
while root:
# 如果左子树不空,则找到左子树的最右节点
if root.left:
pre = root.left
while pre.right:
pre = pre.right
# 将左子树最右节点.right 指向根节点
pre.right = root
# 将root的left置为空并继续往左遍历
tmp = root
root = root.left
tmp.left = None
# 左子树为空,则打印这个节点,并向右边遍历
else:
res.append(root.val)
root = root.right
return res
|
莫里斯遍历-2
通过空闲指针的方式,跟前序版本非常类似,差别是在:
前序遍历时,添加值是在if not tmp.right部分
中序遍历时,添加值是在else部分
前序遍历时,当tmp.right为空时,说明是第一次访问,所以要加入到集合中
中序遍历时,当tmp.right不为空,说明是第二次访问,所以要添加到集合中
Python代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
|
class Solution(object):
def inorderTraversal(self, root):
res = []
while root:
if root.left:
# 找到根节点左子树的最右节点
tmp = root.left
while tmp.right and tmp.right != root:
tmp = tmp.right
# 为空说明是第一次访问
if not tmp.right:
# 并将右节点指向根
tmp.right = root
# 根节点继续往左访问
root = root.left
# 最右节点不空,说明访问过了,要断开
# 同时将值加入到结果集中
else:
res.append(root.val)
tmp.right = None
root = root.right
# 访问根的右边
else:
res.append(root.val)
root = root.right
return res
|
后序遍历
迭代版本
后序遍历是:左节点-右节点-打印根 这种顺序,如果将顺序改为:
打印根-右节点-左节点
再将顺序取反,就变成了:
左节点-右节点-打印根
这正好就是后序遍历的结果。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
class Solution(object):
def postorderTraversal(self, root):
if not root:
return []
res = []
stack = []
pre = None
while stack or root:
# 不断往右子树方向走,每走一次就将当前节点保存到栈中
if root:
res.append(root.val)
stack.append(root)
root = root.right
# 当前节点为空,说明右边走到头了,从栈中弹出节点并保存
# 然后转向左边节点,继续上面整个过程
else:
root = stack.pop()
root = root.left
# 结果集中保存的是[根、右、左],将其反转就是后序遍历
return res[::-1]
|
后序遍历的另一个版本
Python代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
|
class Solution(object):
def postorderTraversal(self, root):
if not root:
return []
res = []
stack = []
pre = None
while root or stack:
# 仍然是不断往左,并不断加入到栈中
if root:
stack.append(root)
root = root.left
else:
# 从栈中弹出,如果右边是空的,或者root.right==pre,
# 说明左右都访问过了,那么就将root.val加入到结果集中
# 1(root)
# / \
# 2 3(pre)
root = stack.pop()
if not root.right or root.right == pre:
res.append(root.val)
pre = root
root = None
# 继续访问右边
else:
stack.append(root)
root = root.right
return res
|
莫里斯遍历-1
跟迭代类似,我们要构造出 [根、右、左] 这种模式,然后取反。
也就是将 根的右节点的最左节点,指向根的右节点,再将根的右节点调整为左节点,并将右节点置为空,伪代码如下:
root.right.最左节点.left = root.left
root.left = root.right
root.right = None
如下图,将6(根节点右子树的最左节点)的left指向根的左边2。
再将1的left指向3,右边置为空。
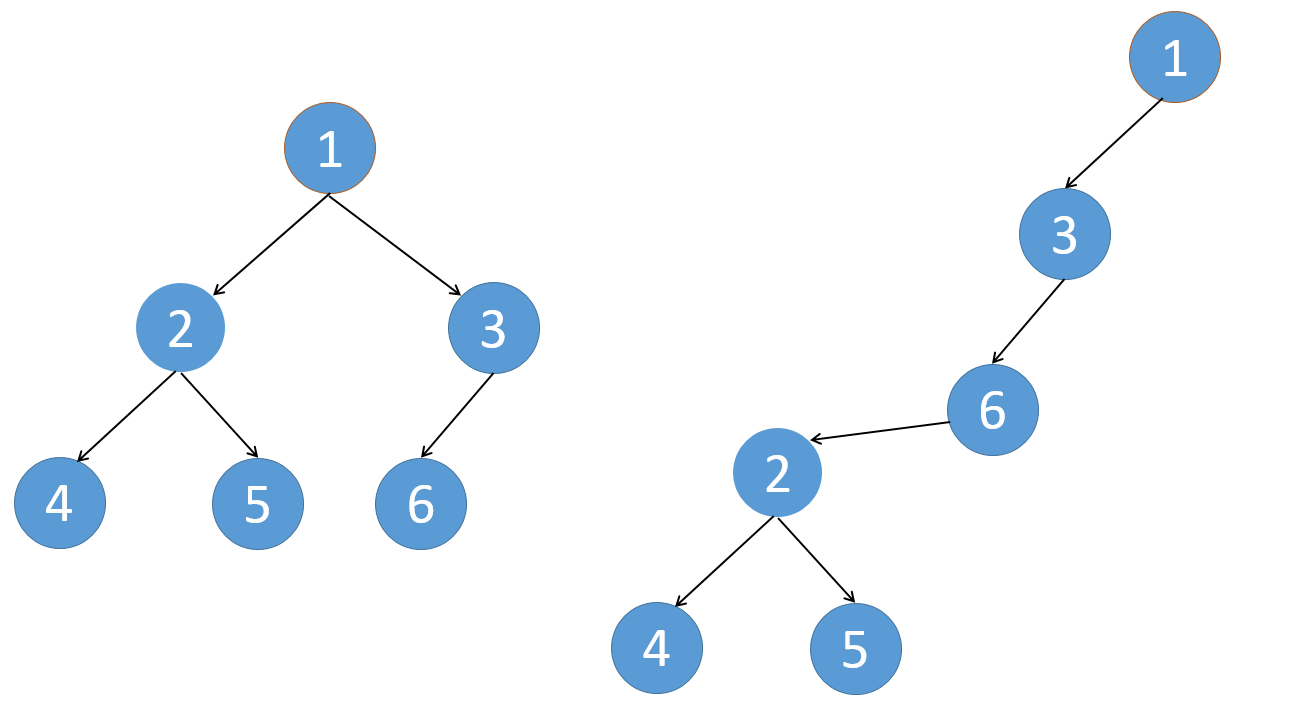
代码整体跟前序很类似,把所有 left 改成了 right
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
class Solution(object):
def postorderTraversal(self, root):
res = []
while root:
# 如果右子树不空,则找到右子树的最左节点
if root.right:
tmp = root.right
while tmp.left:
tmp = tmp.left
# 将右子树最左节点.left 指向根节点的左子树
tmp.left = root.left
# 将右子树调整为左子树,并将右边置为空
root.left = root.right
root.right = None
else:
# 此时树就变成链表了,不断访问左节点即可
res.append(root.val)
root = root.left
# 结果集中保存的是[根、右、左]这种模式,将其反转后就变成了后序遍历结果了
return res[::-1]
|
莫里斯遍历-2
跟前序遍历类似,只是将所有的 left 改成 right。
首先让6(根的右边子树的最左节点)的left指向1
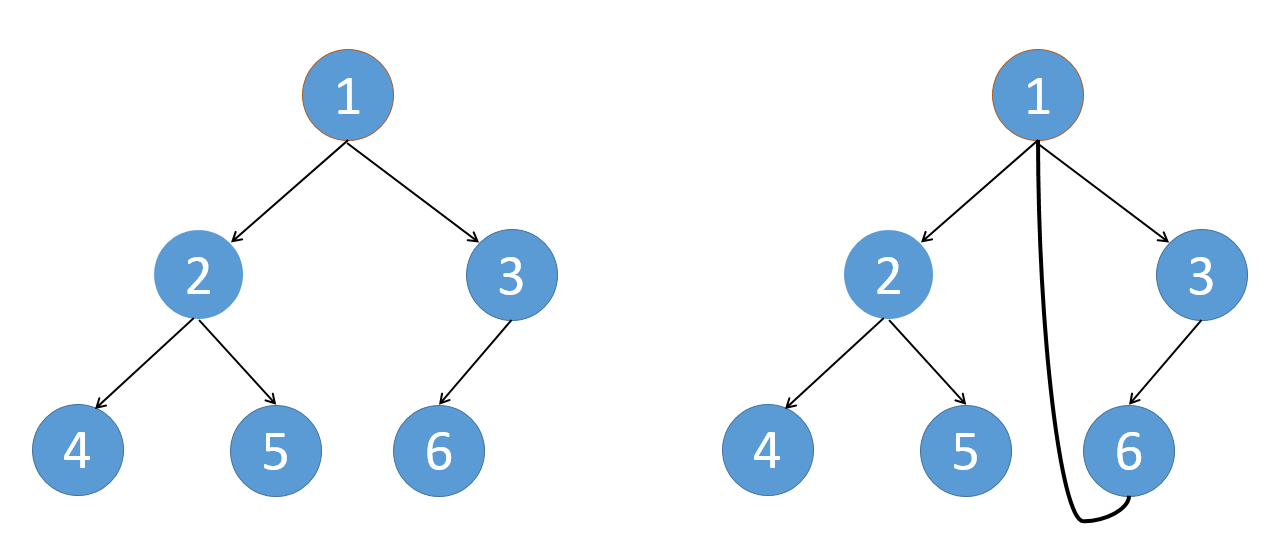
当再次访问节点1时,说明根和其右边都被访问过了,可以将6的left置空。
同理,当再次访问2时,将5的left置空。
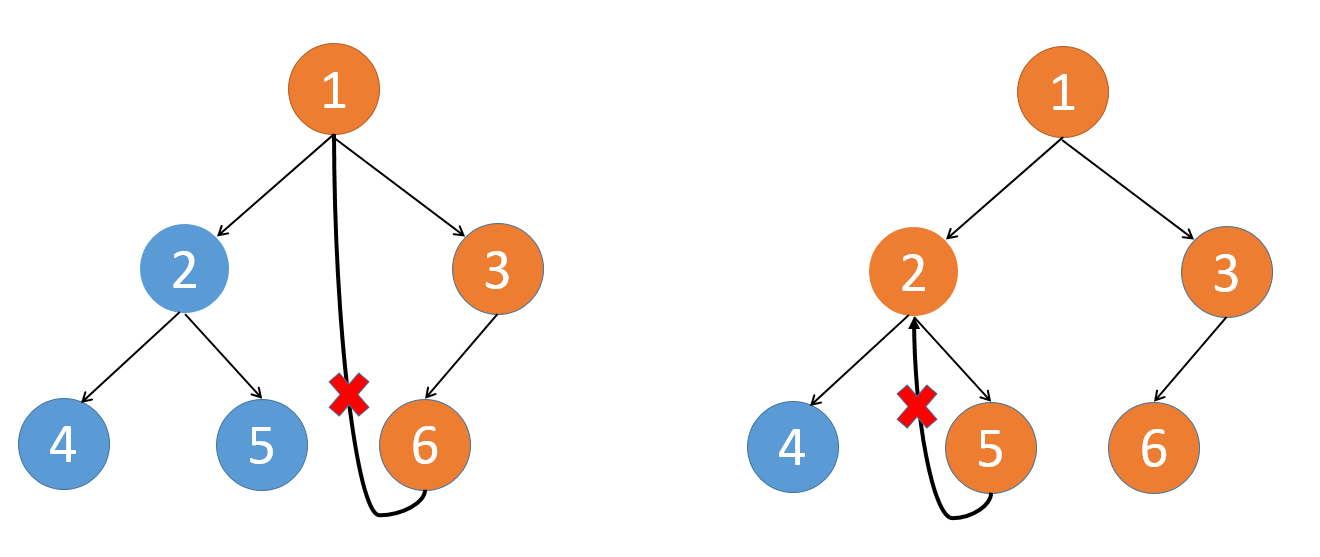
代码:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
|
class Solution(object):
def postorderTraversal(self, root):
res = []
while root:
if root.right:
# 找到根节点右子树的最左节点
tmp = root.right
while tmp.left and tmp.left != root:
tmp = tmp.left
# 找到根节点右子树的最左节点
if not tmp.left:
# 保存到结果集中,并将左节点指向根
res.append(root.val)
tmp.left = root
root = root.right
# 最左节点不空,说明访问过了,要断开
else:
tmp.left = None
root = root.left
# 访问根的左边
else:
res.append(root.val)
root = root.left
# 结果集中保存的是[根、右、左]这种模式,将其反转后就变成了后序遍历结果了
return res[::-1]
|







