马拉车算法

背景介绍

马拉车算法原名叫：Manacher 算法，是一位叫Manacher的人发明的。因为谐音的缘故，被国内程序员戏称为：马拉车算法。
马拉车算法主要用来解决最长回文子串的问题，一般的解法无论是中心探测还是动态规划，时间复杂度都是$O(N^2)$，而马拉车算法可以将时间优化到$O(N)$。

马拉车算法几乎不太可能出现在一般面试当中，是属于程序竞赛范畴的解法。

马拉车算法需要预先对字符串做一些处理，在字符串中插入一些特殊分隔符。
本质上此也是基于中心探测法，但中心探测没有考虑到回文的对称性，做了很多无用功。而马拉车算法在空间上做了很多文章，将之前已经计算过的内容，缓存起来，避免重复的计算，这样就能大幅度提高性能。

首先来回忆下回文串是什么
回文串就是：

bab
aba
上海自来水来自海上

即正着读、反着读都是一样的字符串。
现在给你一个字符串，比如babad，如何求出这个字符串中最长的回文子串呢？
这回就要靠马拉车算法了。

改进中心探测法

先说下中心探测法，这种方法很好理解，以babad这个字符串为例，中心探测法工作原理如下：

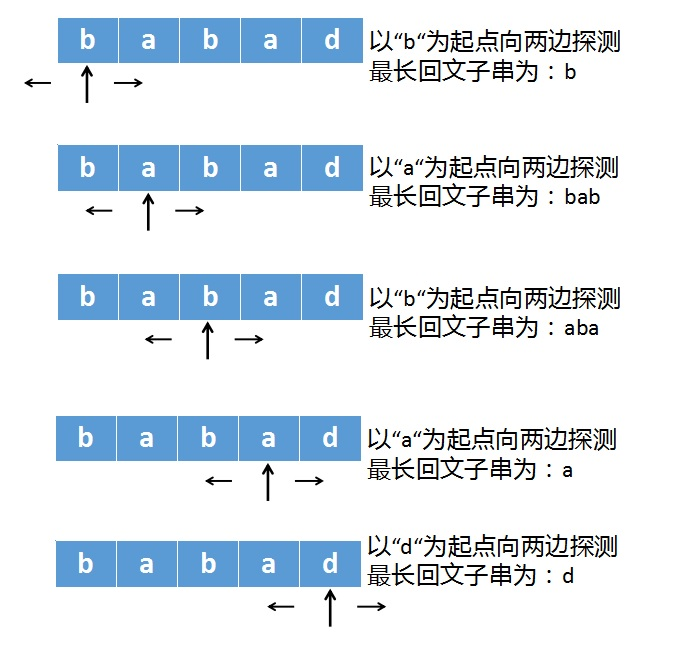
遍历字符串，每遍历到一个字符，就以这个字符为中心，同时往两边扩展，直到两边不等或越界。
根据上述做法，我们就可以求出最长回文串为bab，当时aba也是。

不过上述做法会有个问题，以abb为例，如下图所示：

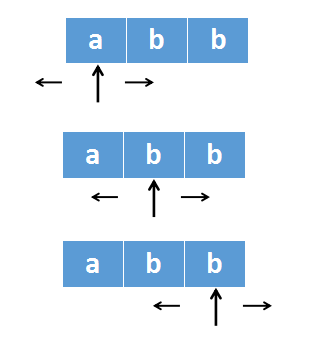
如果以中心探测来计算，最终会得到最长回文串为a，但实际应该是bb

上述做法错误的原因是，没有考虑到回文串的奇偶长度问题。
abbcbba这个字符串长度为7，是以c为中心，两边对称的
而abddbc这个字符串长度为6，是以两个d中间的空隙为中心，两边对称的。
回文串的奇偶性质会导致不同的计算方式。
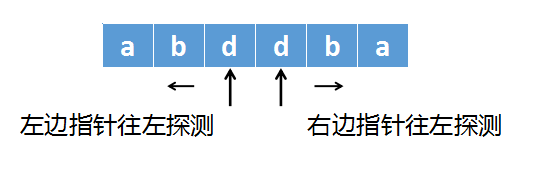
计算第二个字符串时，应当将第一个指针指向左边的d，再将第二个指针指向右边的d，第一个指针往左边探测，第二个指针往右边探测，直到两个指针指向的字符不等、或者越界，如下图所示：

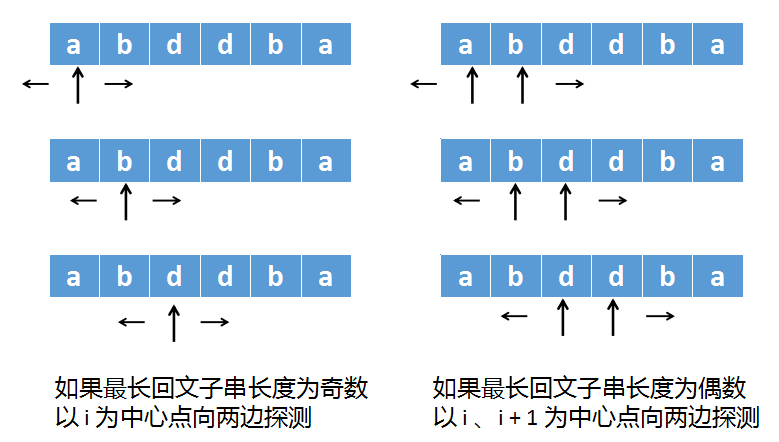
由于我们并不知道最长回文子串到底是奇数长度、还是偶数长度。
所以在计算的时候，需要将奇数和偶数的情况都计算一次，再求一个最大值。

现在我们对原始字符串做一些处理，来解决子串奇偶长度问题，如下图：

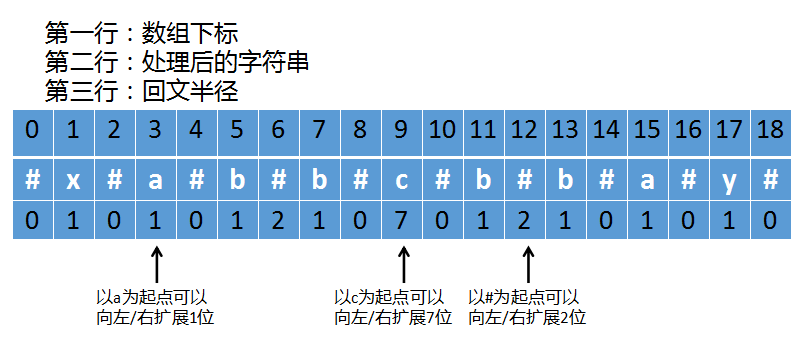
之后我们就可以忽略奇偶长度问题，统一的用中心探测法来求最长回文子串，假设原始字符串为xabbcbbay，经过处理后如下图：

上图中，最重要的是第三行，即回文半径，

最左边的箭头上指向的a这个字符，它可以向左/向右扩展1位，也就是变成#a#这样的回文串，这个字符串总长度是3，以a为中心可以向两边扩展1位(不包括a字符本身)，所以这个字符的回文半径是1。
中间箭头指向的c这个字符，它可以向左/向右扩展7位，即往左是:#a#b#b#，往右是#b#b#a#，以c为中心可以向两边扩展7位(不包括c字符本身)，所以这个字符的回文半径是7。
最右边箭头指向的#这个字符，它可以向左/向右扩展2位，也就是变成#b#b#这样的回文串，这个字符串总长度是5，以#为中心可以向两边扩展2位，所以这个字符的回文半径是2。

好，重点来了。
原始字符是xabbcbbay，它的长度为9。
而经过处理后的字符串#x#a#b#b#c#b#b#a#y#，它的长度为19，也就是说 原字符串长度 * 2 + 1 就等于处理后的字符串长度。
现在计算回文半径时，这个长度不包括箭头指向的字符本身。

那么计算出来的回文半径最大值，就等于原始字符串中最长回文串的长度，即上图中间那个箭头指向的字符c其回文半径长度为7(对应的数组下标是9)，而原始字符串中最长回文串为abbcbba，其长度也是7。
于是我们遍历处理后的字符串，当遍历到下标9时，就会得到计算出最长回文半径7，我们通过下标和回文半径就可以更新start(原始字符最长回文串的起始位置)：

i:当前遍历到的数组下标
armLen:以i为中心，计算出的回文半径
start = (i - armLen) / 2
maxLen = armLen

等字符串全部遍历完，我们根据start和maxLen这两个变量，就可以从原始字符串s中截取出最长回文子串：
s[start : start + maxLen]

我们用#作为分隔符，如果原始字符串中包含了这个字符怎么办呢？
没关系，分隔符可以用任意字符，甚至跟原始字符串中的某个字符重复也可以的，因为我们只是要计算出某个字符的回文半径，并不需要分隔符本身。

由于每遍到一个字符，都需要往左/右进行探测，故这种方式的时间复杂度是$O(N^2)$
空间复杂度是$O(1)$

效率仍然是不高，但是已有有马拉车算法的基本雏形了，后面就是在此基础上做优化，增加辅助空间来优化时间。

代码实现：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41


class Solution {
public:
    string longestPalindrome(string s) {
        if(s.empty() || s.size() < 2) {
            return s;
        }
        //对原始字符串做处理，将abc变成#a#b#c#
        string tmp = "#";
        for(char c : s) {
            tmp += c;
            tmp += "#";
        }
        tmp += "#";
        int n = tmp.size();
        int start = 0;
        int maxLen = 0;
        //从左到右遍历处理过的字符串，求每个字符的回文半径
        for(int i = 0; i < n; ++i) {
            //计算当前以i 为中心的回文半径
            int cur = expand(tmp, i, i);
            //如果当前计算的半径大于maxLen，就更新start(原始字符的起始位置)
            if(cur > maxLen) {
                start = (i - cur) / 2;
                maxLen = cur;
            }
        }
        //根据start和maxLen，从原始字符串中截取一段返回
        return s.substr(start, maxLen);
    }

private:
    //以left和right为起点，计算回文半径，由于while循环退出后left和right各多走了一步
    //所以在返回的总长度时要减去2
    int expand(string s, int left, int right) {
        while(left >= 0 && right < s.size() && s[left] == s[right]) {
            --left;
            ++right;
        }
        return (right - left - 2) / 2;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40


class Solution {
    public String longestPalindrome(String s) {
        if(s==null || s.length() == 0) {
            return "";
        }
        //对原始字符串做处理，将abc变成#a#b#c#
        StringBuilder tmp = new StringBuilder();
        tmp.append("#");
        for(int i = 0; i < s.length(); ++i) {
            tmp.append("#");
            tmp.append(s.charAt(i));
        }
        tmp.append("#");
        int start = 0;
        int maxLen = 0;
        int n = tmp.length();
        //从左到右遍历处理过的字符串，求每个字符的回文半径
        for(int i = 0; i < n; ++i) {
            //计算当前以i 为中心的回文半径
            int cur = expand(tmp, i, i);
            //如果当前计算的半径大于maxLen，就更新start(原始字符的起始位置)
            if(cur > maxLen) {
                start = (i - cur) / 2;
                maxLen = cur;
            }
        }
        //根据start和maxLen，从原始字符串中截取一段返回
        return s.substring(start, start + maxLen);
    }

    //以left和right为起点，计算回文半径，由于while循环退出后left和right各多走了一步
    //所以在返回的总长度时要减去2
    private int expand(StringBuilder s, int left, int right) {
        while(left >= 0 && right < s.length() && s.charAt(left) == s.charAt(right)) {
            --left;
            ++right;
        }
        return (right - left - 2) / 2;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26


class Solution(object):
    def longestPalindrome(self, s):
        if not s or len(s) < 2:
            return s
        # 以left和right为起点，计算回文半径，由于while循环退出后left和right
        # 各多走了一步，所以在返回的总长度时要减去2
        def expand(s, left, right):
            while left >= 0 and right < len(s) and s[left] == s[right]:
                left -= 1
                right += 1
            return (right - left - 2) // 2
        # 对原始字符串做处理，将abc变成#a#b#c#    
        tmp = "#" + "#".join(list(s)) + "#"
        n = len(tmp)
        start = 0
        maxLen = 0
        # 从左到右遍历处理过的字符串，求每个字符的回文半径
        for i in xrange(n):
            # 计算当前以i 为中心的回文半径
            cur = expand(tmp, i, i)
            if cur > maxLen:
                # 如果当前计算的半径大于maxLen，就更新start(原始字符的起始位置)
                start = (i - cur) // 2
                maxLen = cur
        # 根据start和maxLen，从原始字符串中截取一段返回        
        return s[start : start + maxLen]

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39


object Solution {
    def longestPalindrome(s: String): String = {
        if(s == null || s.length < 2) {
            return s
        }
        var tmp = "#"
        for(i <- s.indices) {
            tmp += s.charAt(i)
            tmp += "#"
        }
        var n = tmp.length
        var start = 0
        var max = 0
        //从左到右遍历处理过的字符串，求每个字符的回文半径
        for(i <- tmp.indices) {
            //计算当前以i 为中心的回文半径
            var cur = expand(tmp, i, i)
            //如果当前计算的半径大于max，就更新start(原始字符的起始位置)
            if(cur > max) {
                start = (i - cur) / 2
                max = cur
            }
        }
        //根据start和max，从原始字符串中截取一段返回
        return s.substring(start, start + max)
    }

    //以left和right为起点，计算回文半径，由于while循环退出后left和right各多走了一步
    //所以在返回的总长度时要减去2
    def expand(s: String, _left: Int, _right: Int): Int = {
        var left = _left
        var right = _right
        while(left >=0 && right < s.length && s.charAt(left) == s.charAt(right)) {
            left -= 1
            right += 1
        }
        return (right - left - 2) / 2
    }
}

上面的代码在计算过程中，没有用到辅助空间，计算#x#a#b#b#c#b#b#a#y#中每个字符的回文半径时，都需要往两边扩展一点点计算。
实际上，我们可以将之前计算过的回文半径保存到一个数组中，后面再计算某个字符的回文半径时，就可以利用到之前已经计算过的值。

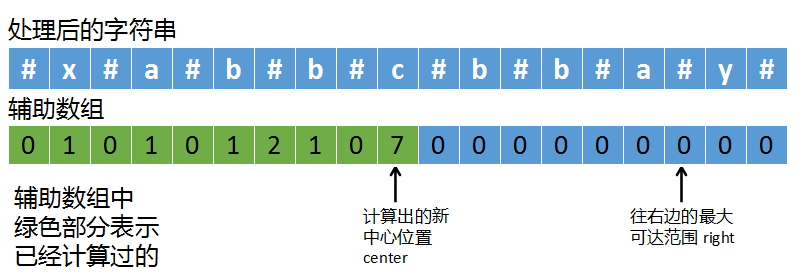如上图，我们需要两个辅助变量：

right，表示已经探测到的字符串最右边的可达范围
center，根据最右边的可达范围的中心对称位置

因为我们是从左往右遍历字符串的，比如当我们计算c这个字符时，可以得知它的回文半径是7，那么就以c为中心点，向右扩展7位，这个位置就是right指向的位置(对应上图中最右边的箭头)。 right这个位置，就是我们目前已经计算出的最右端可达范围，以right和中心对称位置center得到的回文串不一定是最长的，但是right是目前我们能探测到的最远的右端位置。
我们在遍历字符串的同时，也在不断扩大right的范围，right和它的左边都是已经探测过的，right的右边是未探测的。

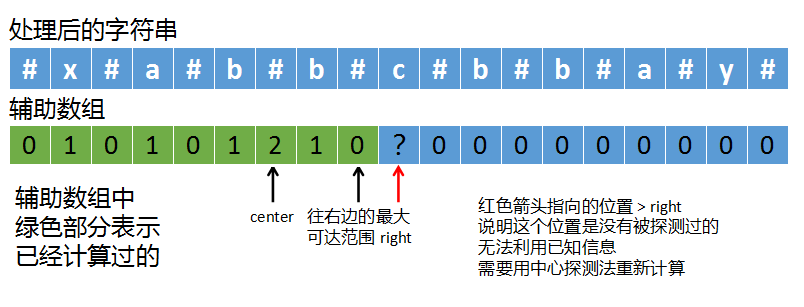上图中，红色箭头指向了#字符，如果用中心探测法计算这个字符的回文半径，我们就得不断往左/右边进行扩展，直到左右字符不等或者越界。

由于是从左往右遍历的，center和right的位置也是根据i来推动的，所以i肯定是大于等于center的。
而回文的特点是左右对称，根据中心位置center，我们就可以找到i的镜像位置，也就是上图中最左边箭头指向的i镜像对称(i_mirror)。

实际上i镜像的值是已经计算过的，它的回文半径是2，那么我们可以根据已知的i镜像的值来计算出i的值。

因为i和i_mirror是根据center对称的，故i + i_mirror = 2 * center，于是可以得到i镜像的下标为：

i_mirror = 2 * center - i

假定数组p中保存了已计算过的回文半径值，那么p[i_mirror]就是i以center为中心镜像对称位置的回文半径长度。

根据数组p[i_mirror]来计算p[i]又分两种情况：

right < i
right >= i

第一种情况right < i，说明要计算的i超过了right的范围，如下如所示：

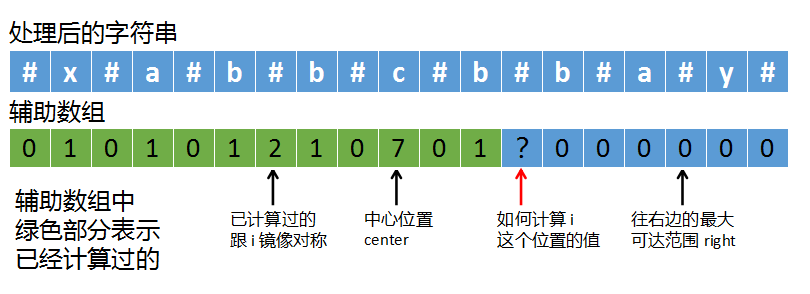
这种情况下，由于i所指向的字符落在right范围之外，说明这个字符没有被探测过，这样的话，就不能再利用已有的信息了，只能用中心探测法，一点一点的向外扩展计算。

第二种情况right >= i，又分细分成三种小情况。
（1）如果right - i > p[i_mirror]

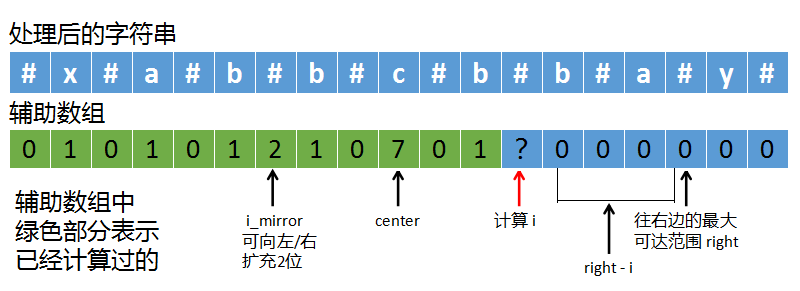
如上图，p[i_mirror]为2，它表示以i_mirror为中心可以向左/右扩展2位。
right - i为4，它表示从i的位置到已探测的最右端right距离为4。

在计算i时，我们可以选择扩展2位，因为i_mirror和i是镜像对称的，p[i_mirror]可以扩展两位，那么i也有可能扩展2位。
也可以选择扩展4位，i到right的距离是4，由right是已探测的最右端位置，那么i-right这段，理论上来说也有可能是回文，所以也有可能扩展4位。

但我们需要选择一个保守的，从上图中也可以发现，如果选择4就不对了，所以当right - i和p[i_mirror]不同时，我们选择较小的那个值。

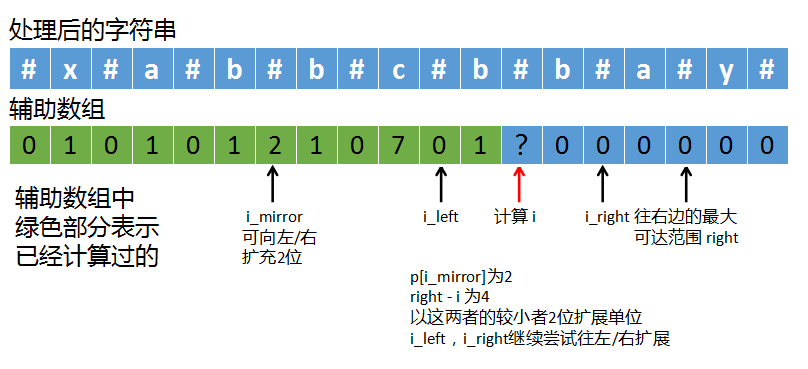
如上图，这次我们在计算i的时候，就不用像中心探测法那样，以i为中心向两边探测了，而是计算出两个新起点i_left和i_right。
i_left就等于i - 2，i_right等于i + 2，这里的2就是p[i_mirror]的值。
我们让i_left和i_right一个往左、一个往右开始探测，这等于是跳过了一些检查的位置，这就是马拉车算法的关键所在，利用已知的i_mirror信息来扩展i，跳过一些已经确定的位置，省去了多余的判断。

（2）如果right - i == p[i_mirror]

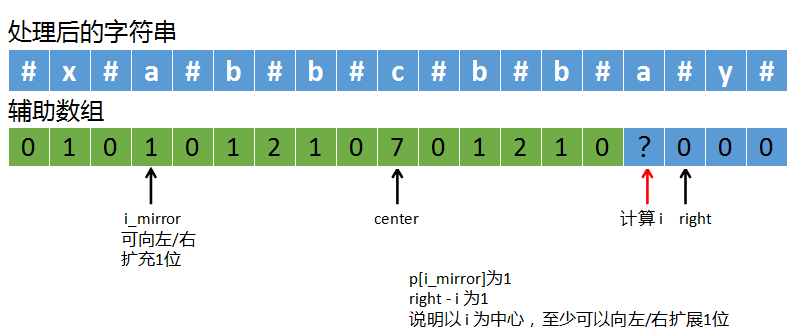
如上图，p[i_mirror]为1，right - i也是为1。
这就说明以i为中心至少可以再向左/右扩展1位。
我们让i_left = i + 1，让i_right = i + 1，然后以i_left和i_right为新起点，继续往左/右扩展。

（3）如果right - i < p[i_mirror]

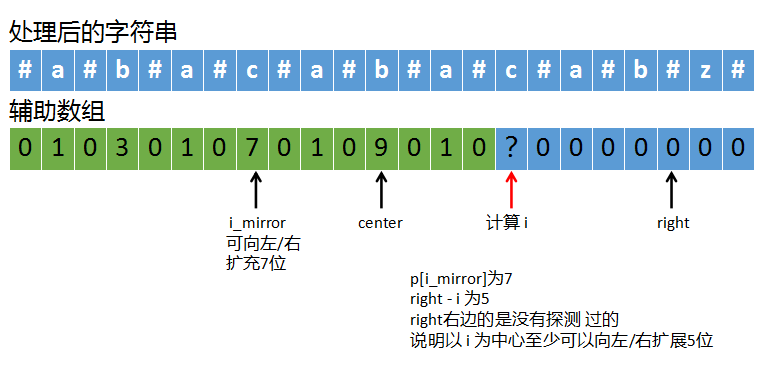
如上图，我们要计算i，此时p[i_mirror]为7，也就是i的镜像位置是可以向左/右扩展7的，但是i可能不行，因为right - i为5，right是我们已经考察过的最右端的位置，i是否可以扩展到right右边我们并不清楚，但是可以肯定是是，至少我们可以向左/右扩展5位，也就是选择right - i和p[i_mirror]中较小的5来扩展。

综上（1）、（2）、（3）我们计算i的回文半径方式如下：

i_mirror = 2 * center - i
最小扩展单位 = min(right - i, p[i_mirror])
以i为中心的回文半径 = expand(i - 最小扩展单位, i + 最小扩展单位)

马拉车算法仍然是外面一个for循环，里面再套了一个while循环。
但对于每个位置i，扩展要么从当前的最右端的right开始，要么只会进行一步，而right最多向前走N，故时间复杂度为：$O(N)$
空间复杂度是：$O(N)$

代码实现：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63


class Solution {
public:
    string longestPalindrome(string s) {
        if(s.empty() || s.size() < 2) {
            return s;
        }
        //对原始字符串做处理，将abc变成#a#b#c#
        string tmp = "#";
        for(char c : s) {
            tmp += c;
            tmp += "#";
        }
        tmp += "#";
        int n = tmp.size();
        //right表示目前计算出的最右端范围，right和左边都是已探测过的
        int right = 0;
        //center最右端位置的中心对称点
        int center = 0;
        int start = 0;
        int maxLen = 0;
        //p数组记录所有已探测过的回文半径，后面我们再计算i时，根据p[i_mirror]计算i
        vector<int> p(n, 0);
        //从左到右遍历处理过的字符串，求每个字符的回文半径
        for(int i = 0; i < n; ++i) {
            //根据i和right的位置分为两种情况：
            //1、i<=right利用已知的信息来计算i
            //2、i>right，说明i的位置时未探测过的，只能用中心探测法
            if(right >= i) {
                //这句是关键，不用再像中心探测那样，一点点的往左/右扩散，根据已知信息
                //减少不必要的探测，必须选择两者中的较小者作为左右探测起点
                int minArmLen = min(right - i, p[2 * center - i]);
                p[i] = expand(tmp, i - minArmLen, i + minArmLen);
            }
            else {
                //i落在right右边，是没被探测过的，只能用中心探测法
                p[i] = expand(tmp, i, i);
            }
            //大于right，说明可以更新最右端范围了，同时更新center
            if(i + p[i] > right) {
                center = i;
                right = i + p[i];
            }
            //找到了一个更长的回文半径，更新原始字符串的start位置
            if(p[i] > maxLen) {
                maxLen = p[i];
                start = (i - p[i]) / 2;
            }
        }
        //根据start和maxLen，从原始字符串中截取一段返回
        return s.substr(start, maxLen);
    }

private:
    //以left和right为起点，计算回文半径，由于while循环退出后left和right各多走了一步
    //所以在返回的总长度时要减去2
    int expand(string s, int left, int right) {
        while(left >= 0 && right < s.size() && s[left] == s[right]) {
            --left;
            ++right;
        }
        return (right - left - 2) / 2;
    }
};

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62


class Solution {
    public String longestPalindrome(String s) {
        if(s==null || s.length() == 0) {
            return "";
        }
        //对原始字符串做处理，将abc变成#a#b#c#
        StringBuilder tmp = new StringBuilder();
        tmp.append("#");
        for(int i = 0; i < s.length(); ++i) {
            tmp.append("#");
            tmp.append(s.charAt(i));
        }
        tmp.append("#");
        int n = tmp.length();
        //right表示目前计算出的最右端范围，right和左边都是已探测过的
        int right = 0;
        //center最右端位置的中心对称点
        int center = 0;
        int start = 0;
        int maxLen = 0;
        //p数组记录所有已探测过的回文半径，后面我们再计算i时，根据p[i_mirror]计算i
        int[] p = new int[n];
        //从左到右遍历处理过的字符串，求每个字符的回文半径
        for(int i = 0; i < n; ++i) {
            //根据i和right的位置分为两种情况：
            //1、i<=right利用已知的信息来计算i
            //2、i>right，说明i的位置时未探测过的，只能用中心探测法
            if(right >= i) {
                //这句是关键，不用再像中心探测那样，一点点的往左/右扩散，根据已知信息
                //减少不必要的探测，必须选择两者中的较小者作为左右探测起点
                int minArmLen = Math.min(right - i, p[2 * center - i]);
                p[i] = expand(tmp, i - minArmLen, i + minArmLen);
            }
            else {
                //i落在right右边，是没被探测过的，只能用中心探测法
                p[i] = expand(tmp, i, i);
            }
            //大于right，说明可以更新最右端范围了，同时更新center
            if(i + p[i] > right) {
                center = i;
                right = i + p[i];
            }
            //找到了一个更长的回文半径，更新原始字符串的start位置
            if(p[i] > maxLen) {
                start = (i - p[i]) / 2;
                maxLen = p[i];
            }
        }
        //根据start和maxLen，从原始字符串中截取一段返回
        return s.substring(start, start + maxLen);
    }

    //以left和right为起点，计算回文半径，由于while循环退出后left和right各多走了一步
    //所以在返回的总长度时要减去2
    private int expand(StringBuilder s, int left, int right) {
        while(left >= 0 && right < s.length() && s.charAt(left) == s.charAt(right)) {
            --left;
            ++right;
        }
        return (right - left - 2) / 2;
    }
}

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45


class Solution(object):
    def longestPalindrome(self, s):
        if not s or len(s) < 2:
            return s
        # 以left和right为起点，计算回文半径，由于while循环退出后left和right
        # 各多走了一步，所以在返回的总长度时要减去2
        def expand(s, left, right):
            while left >= 0 and right < len(s) and s[left] == s[right]:
                left -= 1
                right += 1
            return (right - left - 2) // 2
        # 对原始字符串做处理，将abc变成#a#b#c#
        tmp = "#" + "#".join(list(s)) + "#"
        n = len(tmp)
        start = 0
        maxLen = 0
        # right表示目前计算出的最右端范围，right和左边都是已探测过的
        right = 0
        # center最右端位置的中心对称点
        center = 0
        # p数组记录所有已探测过的回文半径，后面我们再计算i时，根据p[i_mirror]计算i
        p = [0] * n
        # 从左到右遍历处理过的字符串，求每个字符的回文半径
        for i in xrange(n):
            # 根据i和right的位置分为两种情况：
            # 1、i<=right利用已知的信息来计算i
            # 2、i>right，说明i的位置时未探测过的，只能用中心探测法
            if right >= i:
                # 这句是关键，不用再像中心探测那样，一点点的往左/右扩散，根据已知信息
                # 减少不必要的探测，必须选择两者中的较小者作为左右探测起点
                minArmLen = min(right - i, p[2 * center - i])
                p[i] = expand(tmp, i - minArmLen, i + minArmLen)
            else:
                # i落在right右边，是没被探测过的，只能用中心探测法
                p[i] = expand(tmp, i, i)
            # 大于right，说明可以更新最右端范围了，同时更新center    
            if i + p[i] > right:
                center = i
                right = i + p[i]
            # 找到了一个更长的回文半径，更新原始字符串的start位置    
            if p[i] > maxLen:
                start = (i - p[i]) // 2
                maxLen = p[i]
        # 根据start和maxLen，从原始字符串中截取一段返回
        return s[start : start + maxLen]

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62


object Solution {
    def longestPalindrome(s: String): String = {
        if(s == null || s.length == 0) {
            return s
        }
        //right表示目前计算出的最右端范围，right和左边都是已探测过的
        var right = 0
        //center最右端位置的中心对称点
        var center = 0
        var start = 0
        var max = 0
        //对原始字符串做处理，将abc变成#a#b#c#
        var tmp = "#"
        for(i <- s.indices) {
            tmp += s.charAt(i)
            tmp += "#"
        }
        var n = tmp.length
        //p数组记录所有已探测过的回文半径，后面我们再计算i时，根据p[i_mirror]计算i
        var p = new Array[Int](n)
        //从左到右遍历处理过的字符串，求每个字符的回文半径
        for(i <- tmp.indices) {
            //根据i和right的位置分为两种情况：
            //1、i<=right利用已知的信息来计算i
            //2、i>right，说明i的位置时未探测过的，只能用中心探测法
            if(right >= i) {
                //这句是关键，不用再像中心探测那样，一点点的往左/右扩散，根据已知信息
                //减少不必要的探测，必须选择两者中的较小者作为左右探测起点
                var minArmLen = Math.min(p(2 * center - i), right - i)
                p(i) = expand(tmp, i - minArmLen, i + minArmLen)
            }
            else {
                //i落在right右边，是没被探测过的，只能用中心探测法
                p(i) = expand(tmp, i, i)
            }
            //大于right，说明可以更新最右端范围了，同时更新center
            if(i + p(i) > right) {
                center = i
                right = i + p(i)
            }
            //找到了一个更长的回文半径，更新原始字符串的start位置
            if(p(i) > max) {
                start = (i - p(i)) / 2
                max = p(i)
            }
        }
        //根据start和maxLen，从原始字符串中截取一段返回
        return s.substring(start, start + max)
    }

    //以left和right为起点，计算回文半径，由于while循环退出后left和right各多走了一步
    //所以在返回的总长度时要减去2
    def expand(s: String, _left: Int, _right: Int): Int = {
        var left = _left
        var right = _right
        while(left >= 0 && right < s.length && s.charAt(left) == s.charAt(right)) {
            left -= 1
            right += 1
        }
        return (right - left - 2) / 2
    }
}

总结

中心探测法，对于长度为奇数、偶数的回文串需要分别处理。
马拉车算法通过增加额外的分割符，统一了奇数、偶数长度的回文串问题。算法需要增加一个辅助的数组，将之前计算过回文半径保存下来。
当再次计算某个位置的回文半径时，可以充分利用回文的对称性，如计算i的时候，参考了p[i_mirror]的值，也就是i的镜像位置，我们根据已探测的最右端位置right和p[i_mirror]选出了一个最小的探测半径minArmLen。
中心探测时，我们以i为中心，不断的向左减1，向右加1，现在有了minArmLen，我们左边直接从i + minArmLen的位置开始往左，右边直接从i + minArmLen的位置往右，省去了很多不必要的判断，这就是马拉车算法的精髓。

马拉车算法

背景介绍

改进中心探测法

马拉车算法

总结

最近文章

分类

归档

标签

RSS