背景
n 皇后问题 研究的是如何将 n个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
给你一个整数 n ,返回所有不同的 n 皇后问题 的解决方案。
每一种解法包含一个不同的 n 皇后问题 的棋子放置方案,该方案中 'Q' 和 '.' 分别代表了皇后和空位。
示例 1:
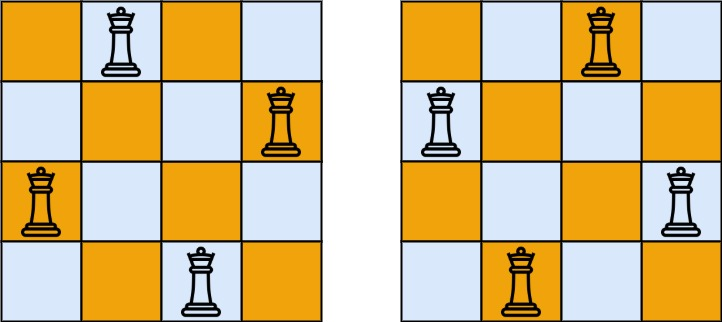
输入:n = 4
输出:[[".Q..","…Q",“Q…”,"..Q."],["..Q.",“Q…”,"…Q",".Q.."]]
解释:如上图所示,4 皇后问题存在两个不同的解法。
示例 2:
输入:n = 1
输出:[[“Q”]]
提示:
1 <= n <= 9
皇后彼此不能相互攻击,也就是说:任何两个皇后都不能处于同一条横行、纵行或斜线上。
解法一
每个皇后可以攻击范围是横着的行,竖着的一列,以及两条斜线
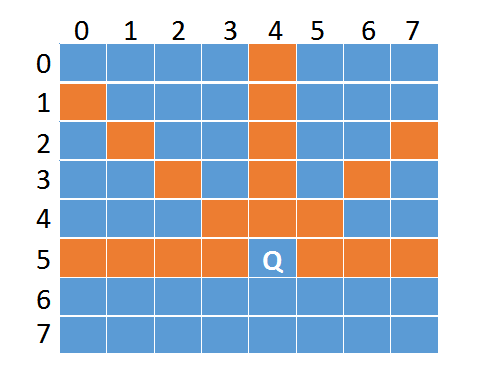
由于一行内不能放置两个皇后,所以我们按行尝试,第一行放置一个皇后、第二行放置一个皇后、第三行放置一个。
具体的摆放过程我们先看一下动画演示
由于回溯的解法8 * 8格子和4 * 4格子都是同样的思路,这里缩小一下规模,我们以4 * 4格的棋盘为例,看下如何摆放皇后使4 * 4格子可以找到一个解。

上图中,我们先在第一行第一列放置一个皇后,这当然是有效的
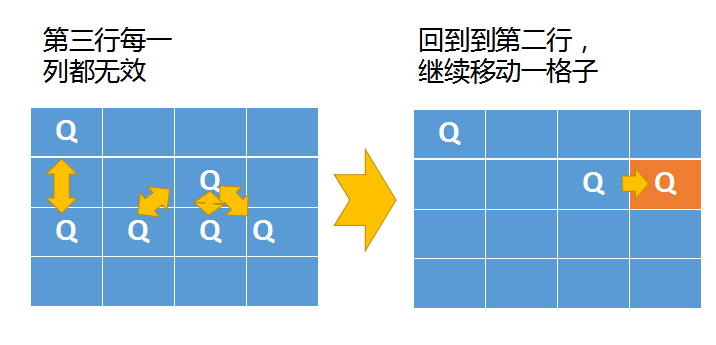
之后尝试第二行第一列(无效),继续尝试第二行第二列(无效),直到第二行第三列
然后再尝试第三行的第一列,此时我们发现第三行的一、二、三、四列都无法放置皇后,于是退回到第二行的第三列,开始尝试第二行的第四列。
第二行的第四列可以放置一个皇后,但继续遍历下去,仍然会走到死胡同,于是继续回退,一直回退到第一行,又开始尝试第一行的第二列。
4 * 4格子的递归调用树如下
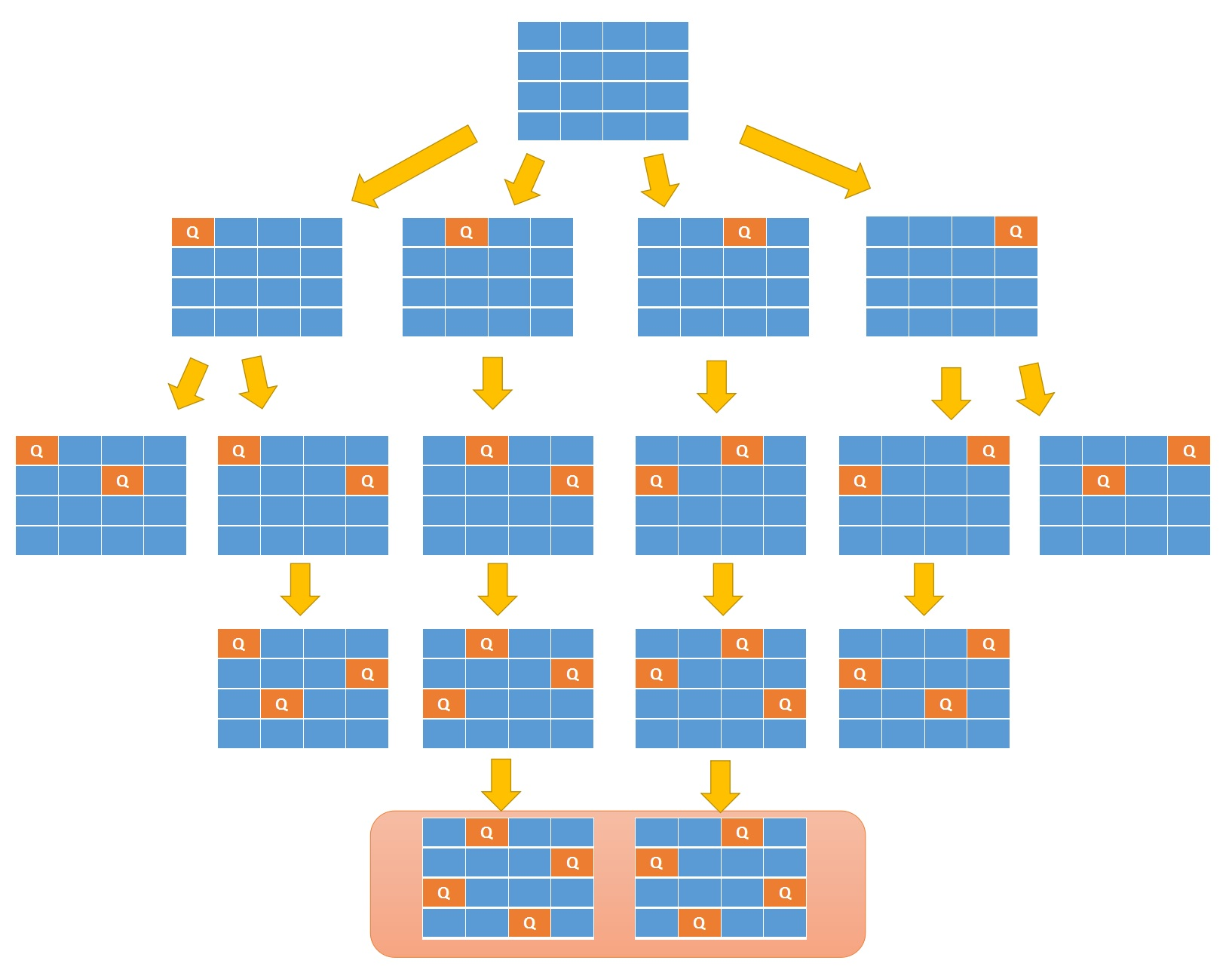
现在我们根据上述的思路写出伪代码
首先我们模拟棋盘格子,生成一个 n * n格子的棋盘,每个格子的值都是"."
我们用x表示行,然后检查行中的每一列y,判断[x,y]这个位置是否可以放置皇后,如果能放置皇后,就将棋盘格[x,y]的位置设置为Q,然后继续尝试下一行。直到x==n,此时所有的皇后都放置完了,那么这时的棋盘就是一个完整的解法,我们直接将此棋盘格子的快照保存下来即可。
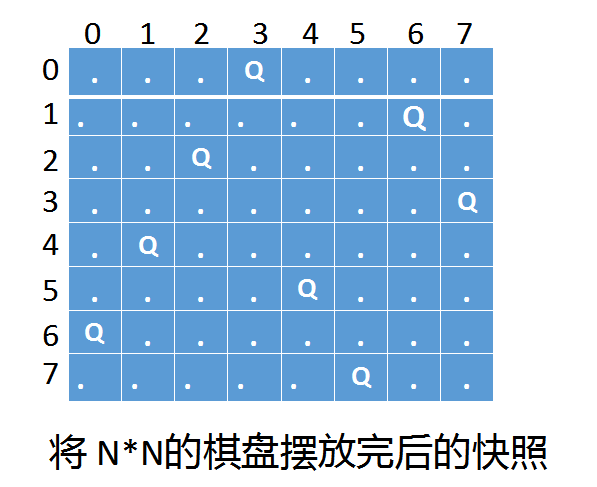
伪代码如下:
dfs函数(x) {
if x==n { //如果x等于n了,说明每行的皇后都放置完毕
//将棋盘内容的快照保存下来
return
}
for(y=0;i<n;++y) {
if [x,y]这个位置是有效的,即横、竖、两个斜线都有没有被攻击 {
将棋盘[x,y]位置设置为 Q
dfs(x+1) 继续尝试下一行
将棋盘[x,y]位置还原
}
}
}
整体的框架我们知道了,现在看下如何检测[x,y]这个坐标位置是否有效
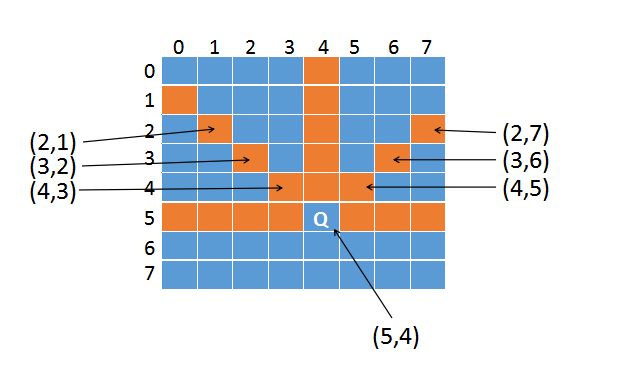
以上图为例,假设我们要检查(5,4)这个位置,由于皇后是按行摆放的,所以就不用检查一行了。
由于是从上到下摆放,第6行、第7行还没有皇后,那么Q往下的竖线,Q往下的斜线都不用检查。
竖线部分只要检查(4,4)、(3,4)、(2,4)、(1,4)、(0,4)这几个位置就可以了。
Q左边那条斜线(从Q位置起(x,y) 对应上图是(5,4)),不断往左上方遍历,坐标变化是(4,3)、(3,2)、(2,1),每次都是x-1,y-1。
Q右边那条斜线(从Q位置起(x,y) 对应上图是(5,4)),不断往右上方遍历,坐标变化是(4,5)、(3,6)、(2,7),每次都是x-1,y+1。
于是我们用三个循环,一个检查竖线、一个检查左边斜线、一个检查右边斜线,就完成了整个校验过程。
代码实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
|
class Solution {
public List<List<String>> solveNQueens(int n) {
//生成N*N的棋盘
char[][] arr = new char[n][n];
//填充棋盘,每个格子默认是“。”表示没有放置皇后
for(int i=0;i<n;++i) {
Arrays.fill(arr[i],'.');
}
List<List<String>> res = new ArrayList<List<String>>();
dfs(arr,0,n,res);
return res;
}
//检查当前的行和列是否可以放置皇后
private boolean check(char[][] arr,int x,int y,int n) {
//检查竖着的一列是否有皇后
for(int i=0;i<x;++i) {
if(arr[i][y]=='Q') {
return false;
}
}
//检查左上到右下的斜边是否有皇后
int i=x-1, j=y-1;
while(i>=0 && j>=0) {
if(arr[i][j]=='Q') {
return false;
}
--i;
--j;
}
//检查左下到右上的斜边是否有皇后
i = x-1;
j = y+1;
while(i>=0 && j<n) {
if(arr[i][j]=='Q') {
return false;
}
--i;
++j;
}
return true;
}
private void dfs(char[][] arr,int x,int n,List<List<String>> res) {
//x是从0开始计算的,当x==n时所有行的皇后都放置完毕,此时记录结果
if(x==n) {
List<String> ans = new ArrayList<String>();
for(int i=0;i<n;++i) {
StringBuilder tmp = new StringBuilder();
for(int j=0;j<n;++j) {
if(arr[i][j]=='.') {
tmp.append(".");
} else {
tmp.append("Q");
}
}
ans.add(tmp.toString());
}
res.add(ans);
return;
}
//遍历每一列
for(int y=0;y<n;++y) {
//检查[x,y]这一坐标是否可以放置皇后
//如果满足条件,就放置皇后,并继续检查下一行
if(check(arr,x,y,n)) {
arr[x][y] = 'Q';
dfs(arr,x+1,n,res);
arr[x][y] = '.';
}
}
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
|
class Solution(object):
def solveNQueens(self, n):
# 生成N*N的棋盘,填充棋盘,每个格子默认是“。”表示没有放置皇后
arr = [["." for _ in xrange(n)] for _ in xrange(n)]
res = []
# 检查当前的行和列是否可以放置皇后
def check(x,y):
# 检查竖着的一列是否有皇后
for i in xrange(x):
if arr[i][y]=="Q":
return False
# 检查左上到右下的斜边是否有皇后
i,j = x-1,y-1
while i>=0 and j>=0:
if arr[i][j]=="Q":
return False
i,j = i-1,j-1
# 检查左下到右上的斜边是否有皇后
i,j = x-1,y+1
while i>=0 and j<n:
if arr[i][j]=="Q":
return False
i,j = i-1,j+1
return True
def dfs(x):
# x是从0开始计算的
# 当x==n时所有行的皇后都放置完毕,此时记录结果
if x==n:
res.append( ["".join(arr[i]) for i in xrange(n)] )
return
# 遍历每一列
for y in xrange(n):
# 检查[x,y]这一坐标是否可以放置皇后
# 如果满足条件,就放置皇后,并继续检查下一行
if check(x,y):
arr[x][y] = "Q"
dfs(x+1)
arr[x][y] = "."
dfs(0)
return res
|
解法二
解法一和解法二的总体思路是类似的,主要差别在于位置判断这块。
解法一中,我们校验[x,y]这个位置是否可以放置皇后,需要三个循环依次判断竖着的一列、左边斜线、右边斜线,效率不太高。
这里我们改用三个集合来判断,一个代表竖着的一列,一个代表左斜线,一个代表右斜线。
竖着的一列好办,只要判断坐标[x,y]中的y是否在集合中就可以了,如果存在表示竖着的这一列曾经摆放过皇后。
我们看下如何处理左边那条斜线(左上到右下)如下图:
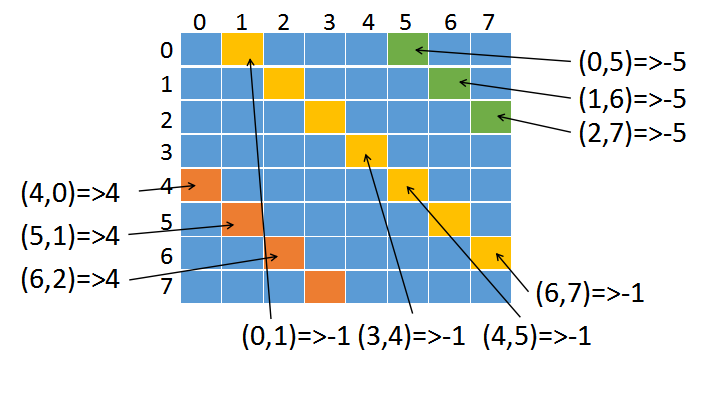
左上到右下的斜线有一个规律,同一条斜线上,x-y得到的值都是相等的
橙色斜线上的四个坐标减出的值都是一样的,同理黄色、绿色也是。
我们只要判断x-y是否在左斜线集合中就可以判断出左斜线上是否有皇后。
右边那条斜线(左下到右上)如下图:
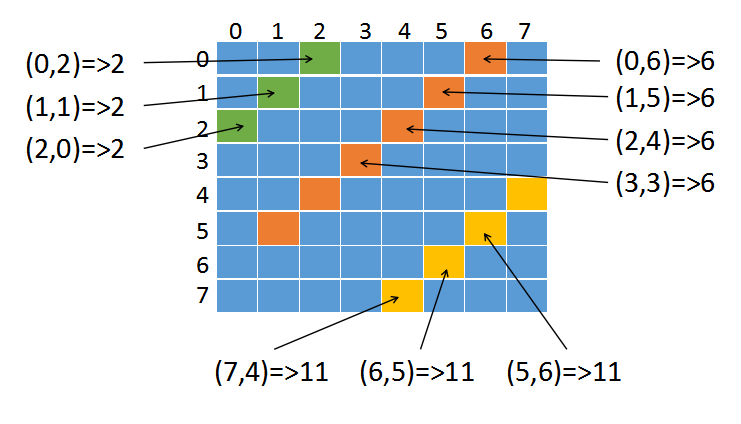
同样也有一个规律,在同一样斜线上,x+y的值是相等的
橙色斜线上的六个坐标加出的值都是一样的,同理黄色、绿色也是。
我们只要判断x+y是否在右斜线集合中就可以判断出右斜线上是否有皇后。
解法一中我们生成了N * N的数组,用来保存棋盘格的快照,这里可以优化成一个N行的数组,数组下标i就对应原先N * N数组中第i行的皇后位置。
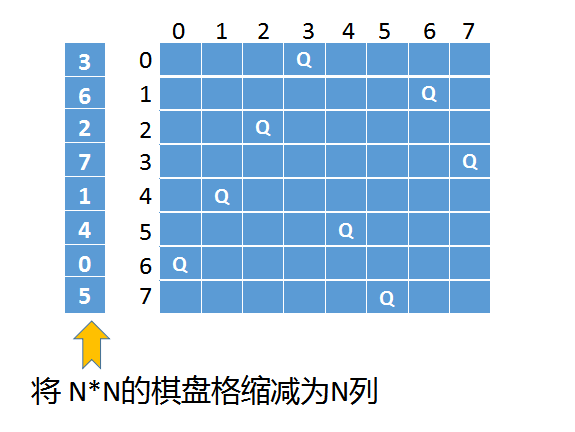
代码实现:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
|
class Solution {
public List<List<String>> solveNQueens(int n) {
//创建一个N行的数组,下标i对应N*N棋盘格子第i行的皇后位置
int[] arr = new int[n];
List<List<String>> res = new ArrayList<List<String>>();
//三个集合,分别判断某一列,左斜线(左上到右下的斜线),右斜线(左下到右上的斜线)
Set<Integer> columns = new HashSet<Integer>();
Set<Integer> hypotenuse1 = new HashSet<Integer>();
Set<Integer> hypotenuse2 = new HashSet<Integer>();
dfs(res,n,0,arr,columns,hypotenuse1,hypotenuse2);
return res;
}
private void dfs(List<List<String>> res,int n,int x,int[] arr,
Set<Integer> columns,Set<Integer> hypotenuse1,Set<Integer> hypotenuse2) {
if(x==n) {
//如果x==n说明所有的皇后都摆放完了
//将arr数组中保存的结果拼接起来
List<String> tmp = new ArrayList<String>();
for(int k=0;k<n;++k) {
char[] row = new char[n];
Arrays.fill(row, '.');
row[arr[k]] = 'Q';
tmp.add(new String(row));
}
res.add(tmp);
return;
}
//遍历一行中的每一列,并检查竖线、左斜线、右斜线是否有皇后
for(int y=0;y<n;++y) {
if(columns.contains(y)) {
continue;
}
if(hypotenuse1.contains(x-y)) {
continue;
}
if(hypotenuse2.contains(x+y)) {
continue;
}
//如果检查通过,设置这一行的皇后位置,并将竖线、左斜线、右斜线的值放入集合中,并继续下一行递归
//当下一层的所有递归遍历完后,回到本轮需要将之前集合、arr数组中保存的结果都清空
arr[x] = y;
columns.add(y);
hypotenuse1.add(x-y);
hypotenuse2.add(x+y);
dfs(res,n,x+1,arr,columns,hypotenuse1,hypotenuse2);
arr[x] = -1;
columns.remove(y);
hypotenuse1.remove(x-y);
hypotenuse2.remove(x+y);
}
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
|
class Solution(object):
def solveNQueens(self, n):
# 创建一个N行的数组,下标i对应N*N棋盘格子第i行的皇后位置
arr = [-1 for _ in xrange(n)]
# 三个集合,分别判断某一列,左斜线(左上到右下的斜线),右斜线(左下到右上的斜线)
columns = set()
hypotenuse1 = set()
hypotenuse2 = set()
res = []
def dfs(x):
if x==n:
# 如果x==n说明所有的皇后都摆放完了
# 将arr数组中保存的结果拼接起来
tmp = []
row = ["."]*n
for k in xrange(n):
row[arr[k]] = "Q"
tmp.append("".join(row))
row[arr[k]] = "."
res.append(tmp)
return
# 遍历一行中的每一列,并检查竖线、左斜线、右斜线是否有皇后
for y in xrange(n):
if y in columns:
continue
if x-y in hypotenuse1:
continue
if x+y in hypotenuse2:
continue
# 如果检查通过,设置这一行的皇后位置,并将竖线、左斜线、右斜线的值放入集合中,并继续下一行递归
# 当下一层的所有递归遍历完后,回到本轮需要将之前集合、arr数组中保存的结果都清空
arr[x] = y
columns.add(y)
hypotenuse1.add(x-y)
hypotenuse2.add(x+y)
dfs(x+1)
arr[x] = -1
columns.remove(y)
hypotenuse1.remove(x-y)
hypotenuse2.remove(x+y)
dfs(0)
return res
|









