Basic Paxos总结

这是 Raft作者介绍 Paxos算法实现的一个视频，在youtube和B站上可以找到
Raft作者Diego Ongaro的youtube频道

The Basic Paxos

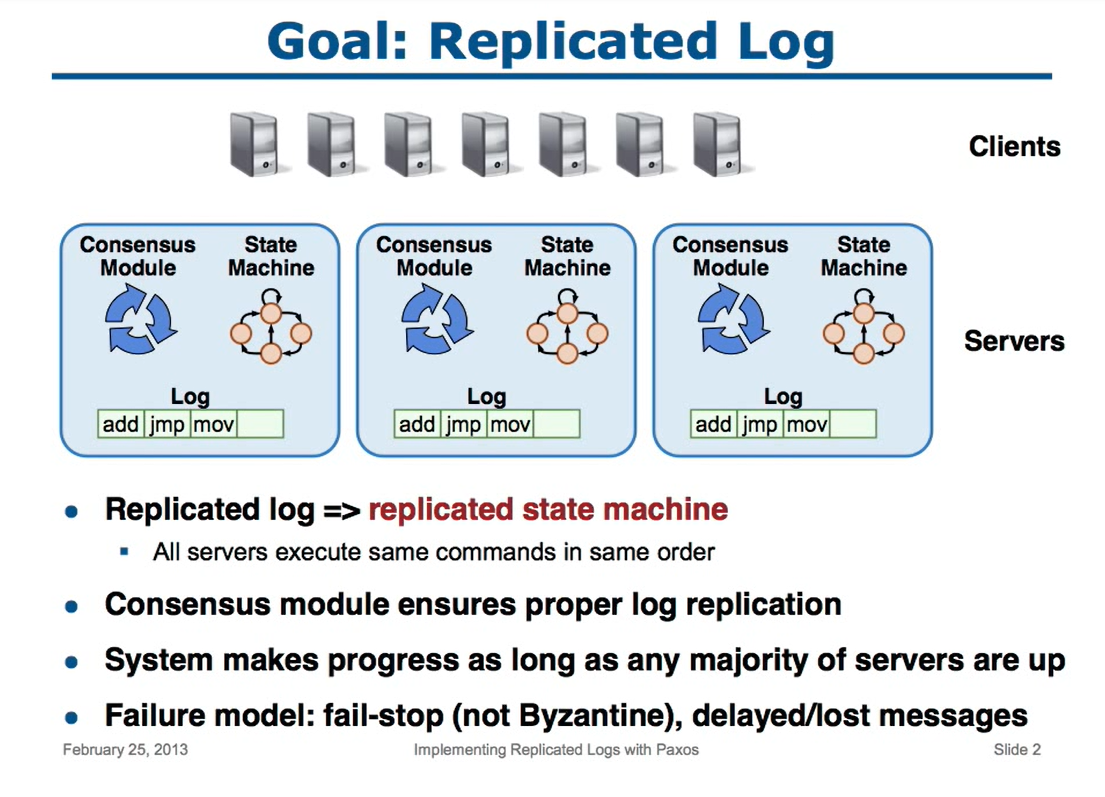
通过实现复制系统的方式来实现Paxos，目标就是维持各个服务器副本相同，从而实现分布式一致性
而保持各个副本的一致性，就是复制状态机，也就是所有的服务器会以相同的顺序执行客户端输入的指令

状态机就是一个程序、应用然后产生一个输出
之后在所有的机器上运行相同的状态机

假设客户端发送一个命令，内容为x
然后收到的机器就在它的本地持久化这个x，并将消息传给其他机器
其他机器也会记录这个x，并执行同样的状态机
等多数派收到反馈后，这个服务端就向客户端返回响应

为保证系统能正确运行，需要收到多数派的反馈

失败模型

消息会丢失，延迟
机器会停止、重启等
但是所有消息都会正确的传递，不会出现拜占庭错误

如果将问题分析，那么 multi-paxos 其实就是执行多次的 basic paxos
而 basic paxos需要有多台机器参与，最多只能选择一个值

Basic Paxos必须满足两个要求

安全性
- 只能选择出一个值
- 如果某个进程认为一个值被选择了，那么这个提案值必须是真的被选择的那个
活性
- 提案最终会被选择
- 其他服务最终会学习到被选择的值

在Paxos论文中，实际是有三个角色

proposer，接收客户端的请求，然后对一个值做提案
acceptor，被动接收消息，并响应共识的投票结果，并将进程的处理状态、选择的值持久化
leaner，学习哪些提案被接受了

为了简化实现，假设只有两个角色，提案者和接受者，并且每个实例都可以同时为这两个角色

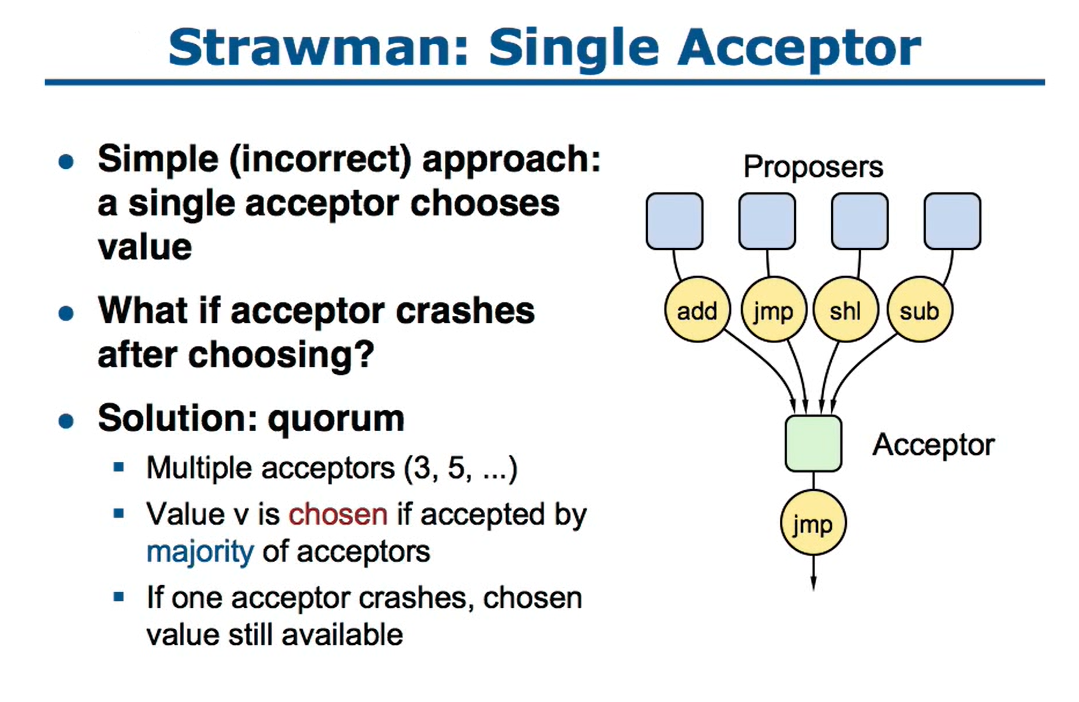单个acceptor实现非常简单，接受多个proposer的提案后做出选择即可
但这种实现也很明显，一旦宕机就不行了
所以为了应对可靠性，必须要有多个acceptor，比如3、5、7等等
这样的话，即使部分节点失效，整个集群仍然可以工作

split votes问题

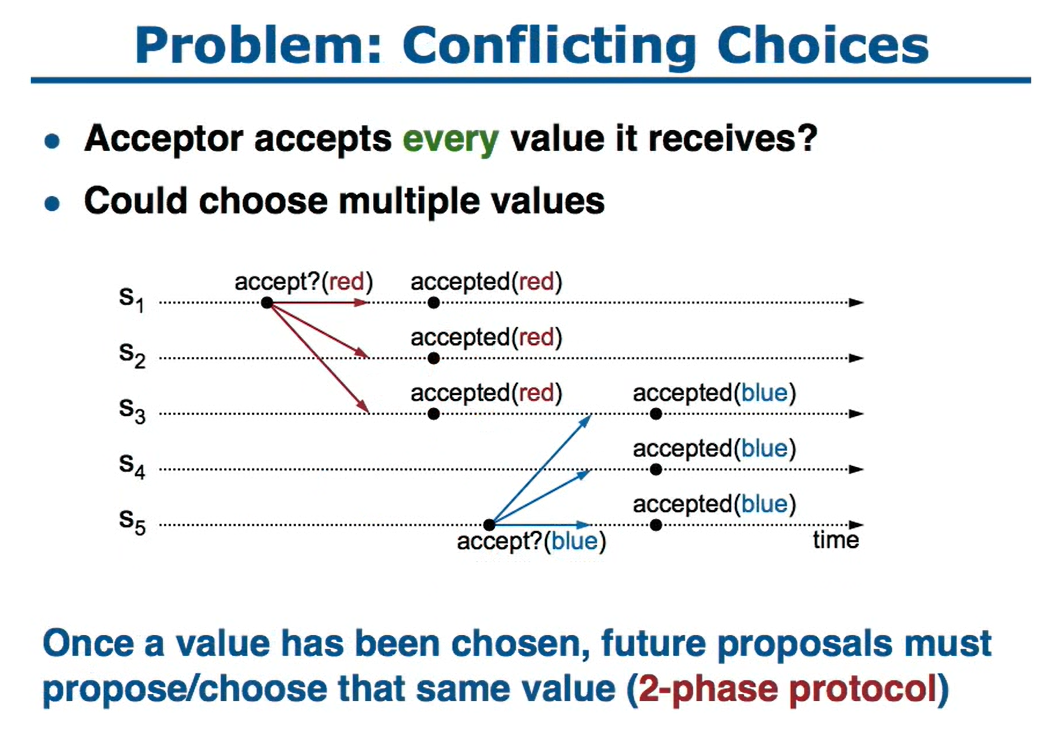
这里假设了，如果acceptor 接受它收到的第一个值
在这种情况下，无法达成多数派
上图中就出现了三派，没有一派是满足的
所以，acceptor必须能接受多个值，也就不同的value

conflicting choices

这里假设acceptor可以接受每次收到的值
这样也会出现问题，第二次会把第一次的给覆盖掉
这种方式不会出现split votes，但不满足安全性
如果一个值被选择了，那么后面的提案内容也必须是这个值
从split votes、conflicting choices可以发现，必须使用两阶段协议

两阶段提交的问题

单纯的两阶段提交也会有问题
比如s5作为proposer提交了bule
此时s5还没有发出accept请求，所以这些blue值还没被chosen
之后s1发出了accept请求，内容是red，而s3的内容把前面的blue覆盖掉了
所以必须要有一种机制，能让s3拒绝掉提交的值
这就需将提案号排序，拒绝掉旧的提案号

为了能对proposal排序，我们就要生成一个唯一的ID

ID由高低位组成；高位的优先级 > 低位
新的proosal编号必须大于之前使用过的编号
低位的ID，可以使用server id
高位的ID使用 round number，这样高位可能会重复，但低位肯定不同
同时要将 max round做持久化存储，是目前的最大轮次编号
proposer宕机或者重启后，round number要增加，不能跟之前重复
ID: Round Number + Server Id

Basic Paxos要做的事情

第一阶段，广播 prepare RPC请求
- 通过这个请求，可以找到已经被chosen的value，这样后面再提交的时候就用这个chosen的value
- 也可以阻止那些还么有完成的proposal，也就是提案号比当前小的
第二阶段，广播 accept RPC请求，让所有的接受者accept这个指定的value

Basic Paxos 算法执行过程

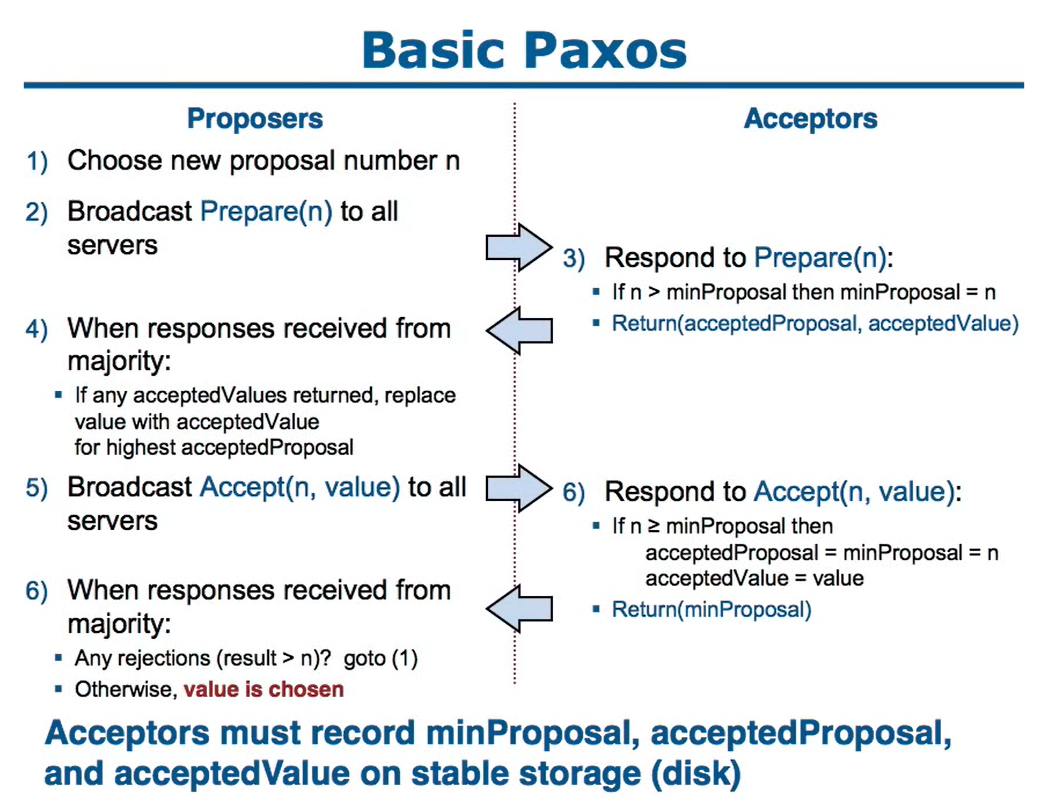
Basix Paxos算法执行过程

第一阶段，prepare阶段：

proposer要选择一个提案号，这个提案号应该是唯一的
发送 prepare请求，将prepare(n) 广播给所有server(除了它自己)
acceptor收到请求后，用 n 跟当前记录的max编号最对比

if n > max: max = n，return(提案编号，value/如果有的话)
if n <= max: 不再接收小于等于n的parepare请求
if n < max: 不再接受小于n的acceptor请求
max 需要持久化

当收到大多数响应后：

if 返回的响应中有value，使用最高编号的value替换掉将要提案的value

第二阶段，accept阶段：
5. 广播 accept(n，value) 到所有的服务器(除了自己)
6. acceptor接受响应

if n >= max
acceptedProposal = max = n
acceptedValue = value
else: 拒绝
acceptedProposal、acceptedValue持久化
return(max)

当收到了大多数响应后

if result(n) > n? 表示拒绝，goto(1)重试
表示value已经被chosen

为了可靠性，acceptor的max、acceptedProposal、acceptedValue 需要持久化
这样即使重启，也不会有问题

伪代码
proposer部分：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12


// prepare   
send PREPARE(++n)   

// prepare receive and send accept request
did I receive PROMISE responses from a majority of acceptors?
if yes
    do any responses contain accepted values (from other proposals)?
    if yes
        val = accepted_VALUE    // value from PROMISE message with the highest accepted ID
    if no
        val = VALUE     // we can use our proposed value
    send Accept(ID, val) to at least a majority of acceptors

acceptor部分：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18


// response prepare
if (n > max_n)
    max_n = n     // save highest n we've seen so far
    if (proposal_accepted == true) // was a proposal already accepted?
        respond: PROMISE(n, accepted_N, accepted_VALUE)
    else
        respond: PROMISE(n)
else
    do not respond (or respond with a "fail" message)
	
// response accept 
if (n >= max_n) // is the n the largest I have seen so far?
    proposal_accepted = true     // note that we accepted a proposal
    accepted_N = n             // save the accepted proposal number
    accepted_VALUE = VALUE       // save the accepted proposal data
    respond: Accepted(N, VALUE) to the proposer and all learners
else
    do not respond (or respond with a "fail" message)	

example

这里展示了三种冲突情况
值已经被chosen
比如 s1 先执行了prepare、然后又执行了accept，于是 n=3.1，value=x
之后 s5 又执行了一个prepare，对于 s3来说，4.5 > 3.1 所以接受了这个请求
并将已经chosen的值 x 返回给 s5
这样，s5 第二次执行accept时，就会发送 accept(4.5,x)，然后多数派响应成功
n=4.5,value=x 就被chosen了

需要注意的是，在上图中，出现了部分节点number不同的情况

s1、s2的编号为 3.1，他们已经accept了
而s3、s4、s5 也accept了，这些的值都是一样，但是编号不同
即使 s4、s5宕机了，集群仍然可以工作
如果有一个新的编号更高的proposal出现了，然后发送给s3、s4、s5
这样就会将这3台机器的编号做更新，于是他们又保持一样了

之前的值没有被chosen，但是新的proposer看到了

比如 s1 提案了 3.1和 x，由网络延迟 s1和s2没有确定，所以这个值没有被chosen
此时s5 也发送了提案 4.5和y，这时s3返回了响应，已经接受
于是 s5 再次 accept时，就会使用之前chosen的value x
最后返回多数派接受，于是n=4.5,value=x 就被chosen了
跟前面一个例子类似，这里也出现了 vlaue一样，但是number不同的情况
即使出现s3、s4宕机，编号最高的仍然是4.5，等下次proposer时这个编号就会被纠正

前面的值没有被chosen，新的proposer也没看到

在这种情况下，第二次会先prepare、然后accept
注意上图中， s3的时间点上，A 4.5之前，s1提交了一个accept
此时因为编号过低，被拒绝了，这样的话，s1的提案就被拒绝了
而s5可以成功chosen，得到了多数派的响应
在chosen之后，各个acceptor的值不相同s1、s2是x，而s3、s4、s5是y
假设此时 s5宕机，那么有两个x、两个y，是否就无法形成多数派呢了？
并非，因为acceptor是可以多次接受值的
那么下次再提案，这4个机器都accepted了，所以会返回x、y
因为4.5 编号更好，所以提案者选择了y，这样再次提案后值就全部变成y了
虽然短时间内可能不同的acceptor值不同，不过再次提案后，他们的值会变成一致

活锁问题

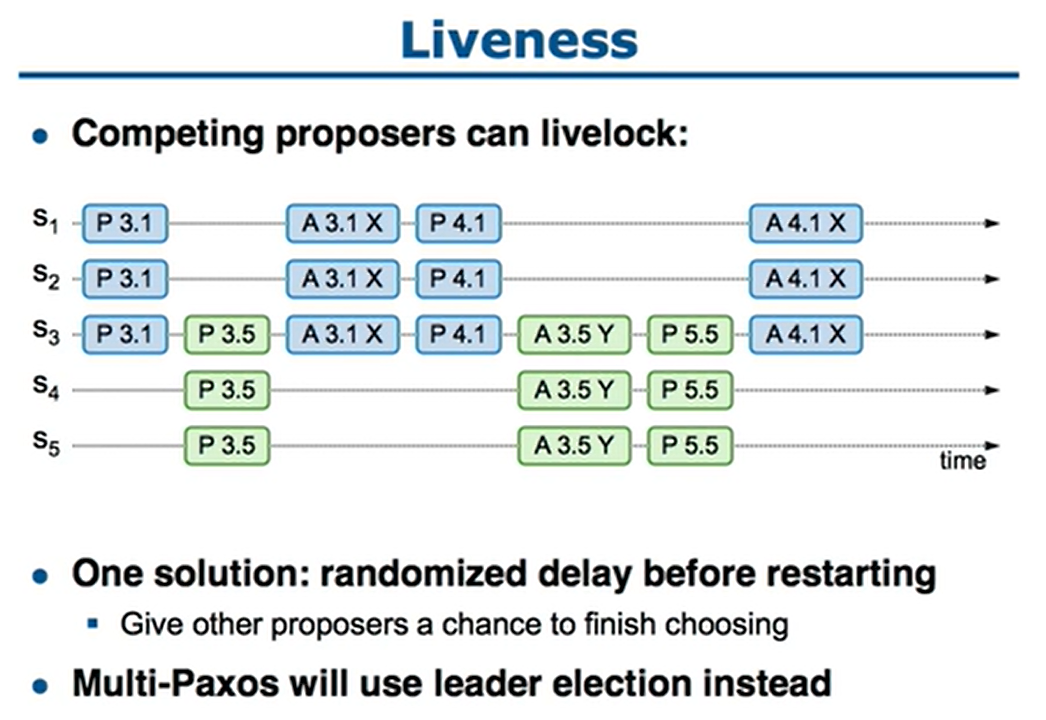
s1的prepare成功了，然后s5又提交了一个编号更高的prepare
于是s1再次accept时就会拒绝，之后s1又立刻准备了一个编号更高的提案去prepare
而这样会把s5的accept拒绝掉，于是s5又立提交了一个更高编号的提案去prepare
这样无穷无尽下去，就变成活锁了
解决方案是，当提交被拒绝后，就等待一个随机的时间，这样可以让其他的机器可以有机会提交成功
另一个方式是使用multi-paox，也就是只有一个 proposer

注意事项

在basic paxos中，只有提案者才知道哪个值被选择了
如果其他服务想知道某个值是否被选择了，它们就需要执行一个Paxos提案
因为从上面例子能发现，有出现split value的情况，这样当多数派返回时，就能确定某个值被chosen

References

[1] Michael J. Fischer, Nancy Lynch, and Michael S. Paterson. Impossibility of distributed consensus with one faulty process. Journal of the ACM, 32(2):374–382, April 1985.
[2] Idit Keidar and Sergio Rajsbaum. On the cost of fault-tolerant consensus when there are no faults—a tutorial. TechnicalReport MIT-LCS-TR-821, Laboratory for Computer Science, Massachusetts Institute Technology, Cambridge, MA, 02139, May 2001. also published in SIGACT News 32(2) (June 2001).
[3] Leslie Lamport. The implementation of reliable distributed multiprocess systems. Computer Networks, 2:95–114, 1978.
[4] Leslie Lamport. Time, clocks, and the ordering of events in a distributed system. Communications of the ACM, 21(7):558–565, July 1978.
[5] Leslie Lamport. The part-time parliament. ACM Transactions on Computer Systems, 16(2):133–169, May 1998.

文章

The Basic Paxos

Basic Paxos 算法执行过程

example

References

最近文章

分类

归档

标签

RSS