原文
http://www.cs.columbia.edu/~kar/pubsk/simd.pdf

背景

现代CPU出现了 SIMD这种并行化的指令，可以用一条执行执行多个数据
通过每条指令消费多个数据，实现加速
SIMD一般用于多媒体、视频领域，这种需要有大量的重复计算
数据库中也有很多大量重复的操作，这就是 SIMD大展身手的好地方了

SIMD指令中有一个不太明显的好处

  • 可以用SIMD指令实现算数操作，来避免条件分支
  • 现代CPU中都有很长的流水线
  • 如果分支预测失败，则会flush掉整个操作，会出现等待，导致性能下降

论文中实现了一些重要的数据库操作

  • index scan
  • agg
  • index
  • join

以下就是一个 SIMD指令，两个操作源都是 128位的寄存器，都是包含了 4个单精度的float类型
目标寄存器中分别保持了 4个单精度的结果集

  • x1 and y1
  • x2 and y2
  • x3 and y4
  • x4 and y4
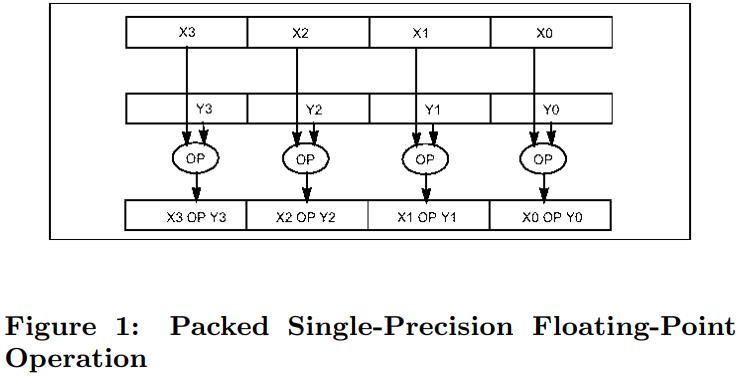
    这种是 Intel指令集，如果是其他的平台也是类似的
    SIMD还包含其他操作，比如算数操作、比较操作、转换操作、逻辑操作等
    上述的并行度为4

Vector processors vs SIMD

  • vector处理器一般包含 64 - 512个 64bit元素，而SIMD一般包含4个元素
  • 因此vector的并行度更高
  • 但vector的load、store延迟更高
  • SIMD指令在超标量流水线中有优势，可以跟其他指令重叠工作

编译器可以自动将 普通code转换为SIMD代码，但也有限制

  • 比如使用了全局指针、复杂一点的表达式
  • 数据是否对其
  • 循环中的非对其声明

不同平台的限制也不同，所以有时候 DB开发者需要向多媒体编程一样，显示的利用 SIMD指令

128位bit(包含4个32位值) op 128位bit，其结果也是 128位
如果是比较操作，那么128位结果中，就包含4个结果值，每个值都是 0xFFFFFFFF，或者全0
SUN，或者MIPS都支持bit向量结果，Intel和AMD也支持，就是将结果的最高有效位拷贝到bit中即可
这个指令叫做：SIMD_bit_vector

数据对其也必须考虑，虽然SIMD也支持不对齐的拷贝，但是不对齐的效率明显低于 对齐的
可以使用列存来解决这个问题

分支预测错误的代价很高，大概会有20个时钟周期的延迟
而即使只有 5%的预测错误，也会有 20% - 30%的性能下降

两个主要的优化思路

  • 使用SIMD指令实现并行化处理
  • 避免分支预测失败

scan操作

需要考虑到 输入数据对其问题，可能需要提前处理一下
输入数据的size可能不是 W(SIMD宽度)的倍数，所以结尾需要再单独处理一下

一段普通的标量伪代码如下： N 是输入元素，它是SIMD宽度的倍数，x、y是输入记录的列数组
一般列扫描可能需要扫描多列，这里为了简化只使用了一个列

1
2
3
4
5
6

for i = 1 to N {
	if (condition(x[i])) then 
		process1(y[i]);
	else 
		process2(y[i]); 
}

与此对应的 SIMD 风格的伪代码如下：

1
2
3
4

for i = 1 to N step S {
	Mask[1..S] = SIMD_condition(x[i..i+S-1]);
	SIMD_Process(Mask[1..S], y[i..i+S-1]); 
}

假设 if 条件为 (4 < x) && (x <= 8)
那么对应的 SIMD方式为 (4 SIMD_ < x) SIMD_AND (x SIMD_ <= 8)
SIMD指令的数据类型都是定长的，因此很难实现 SQL LIKE 这样的操作

Return the First Match

假设 process1(y)的实现如下：

1
2
3
4

process1(y) { 
	result = y; 
	return; 
}

也就是当 x[i] 满足时，返回第一个 y[i]
对应的 SIMD版本为：

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

SIMD_Process(mask[1..S],y[1..S]) {
	V = SIMD_bit_vector(mask);
	/* V = number between 0 and 2^S-1 */
	if (V != 0) {
		for j = 1 to S {
			if ( (V >> (S-j)) & 1 ) { /* jth bit */
				result = y[j]; 
				return; 
			} 
		}
	}	
}

if(v != 0) 是一个优化，如果选择率比较低，掩码总是 0，则可以跳过 if
之后开始遍历，如果向量寄存器为 128，输入的是32bit，则遍历 4次
V 包含了 4组掩码
(V » (S - j)) & 1) 将掩码内容不断右移，然后跟 1 做与，如果结果为0说明这个掩码不满足
继续测试，直到某个掩码位是 1，那么对应的 y[i] 就是第一个满足条件的，返回即可
唯一匹配，一般是 B+树搜索叶子节点时，此时的值都是唯一的

改进后的，把for循环的次数变成了对数

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

SIMD_Process(mask[1..S],y[1..S]) {
	V = SIMD_bit_vector(mask);
	/* V = number between 0 and 2^S-1 */
	if (V != 0) {
		result = SIMD_And(mask,y);
		for j = 0 to log_2(S)-1 {
			result = SIMD_Or(result, SIMD_Rotate(result,2^j));
		}
		return result[1]; 
	}
}

SIMD版本比原始版本有 3倍的提升

Return All Matches

返回全部匹配元素，普通版本如下
pos指向result数组的开头

1
2
3

process1(y) {
	return[pos++] = y;
}

SIMD实现类似，这里称为方案 1

1
2
3

{ 
	result[pos++] = y[j]; 
}

方案2 如下

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

SIMD_Process(mask[1..S], y[1..S]) {
	V = SIMD_bit_vector(mask);
	/* V = number between 0 and 2^S-1 */
	if (V != 0) {
		for j = 1 to S {
			tmp = (V >> (S-j)) & 1; /* jth bit */
			result[pos] = y[j];
			pos += tmp; 
		} 
	}
}

第一个版本是带有 if的，如果出现分支预测失败则代价很高
第二个虽然有额外的拷贝，但是消除了分支

下图是查找SELECT y FROM R WHERE x_low < x <x_high这样的语句
SIMD明显是要快很多，但是版本2更好，因为分支预测的影响， 以及更高的并行性

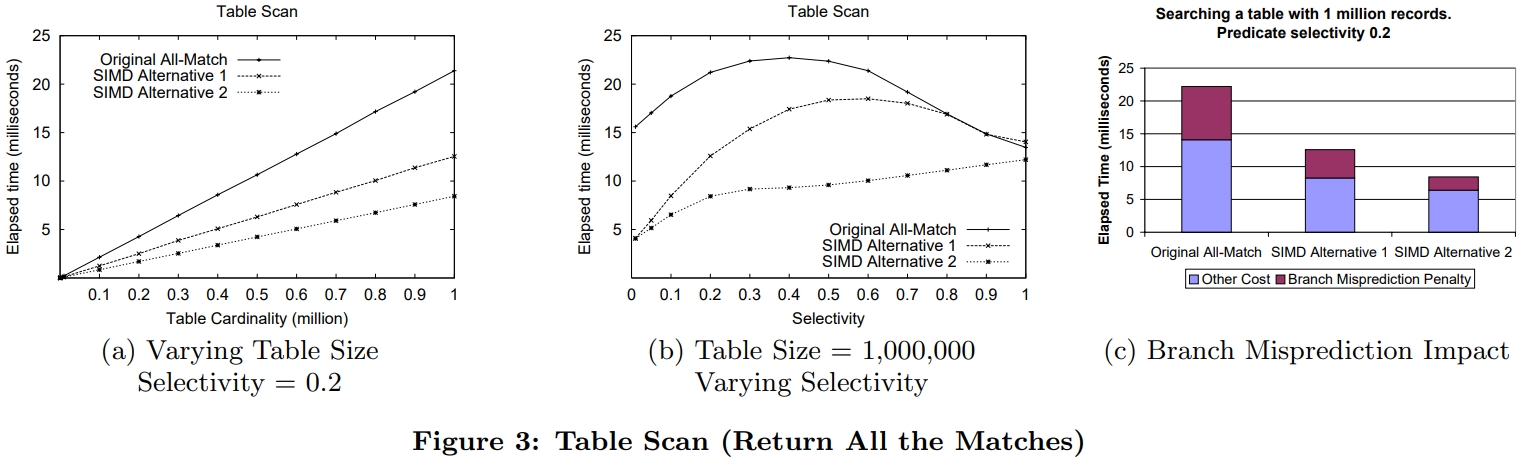
只要把 find all match 的逻辑稍微修改一下，就可以生成 bitmap 索引了

Scalar Aggregation

Sum and Count
如果想对满足某一行中的 y列做聚合，用SQL表示就是一个普通的聚合，不需要group by
group by可以用排序实现
对于标量版本 sum 实现如下：

1
2
3

process1(y) {
	result = result + y;
}

SIMD 版本的sum如下：

1
2
3
4

SIMD_Process(Mask[1..S], y[1..S]) {
	temp[1..S] = SIMD_AND( Mask[1..S], y[1..S] );
	sum[1..S] = SIMD_+( sum[1..S], temp[1..S] );
}

对于不满足条件的元素，对应的 掩码 mask[i]被设置为0，然后做 AND运算，将其记录到tmp变量中
这样不满足的y[i] 对应的 tmp[i] 就是0，不影响结果
之后再做 SIMD累加，结果就保存到 sum中，在通过 log_2(S)做rotate将sum元素累加，就是最终结果

Min and Max
SIMD指令中包含了 min、max相关的操作，利用这一点就可以实现 min()、max()这种聚合函数
这里定义一个 min数组，初始元素都是 infinity 无穷大
然后做掩码匹配，筛选出匹配的元素，对那些不匹配的元素，赋 infinity，这样就不影响最小值了
之后最小元素就存于 min数组中，然后使用 log_2(S)的方式 rotate，循环SIMD位宽S，就降低为对数次

1
2
3
4
5
6

SIMD_process(mask[1..S], y[1..S]) {
	temp1[1..S] = SIMD_AND( mask[1..S], y[1..S] );
	temp2[1..S] = SIMD_ANDNOT( mask[1..S],infinity[1..S] );
	temp1[1..S] = SIMD_OR( temp1[1..S], temp2[1..S] );
	min[1..S] = SIMD_MIN( min[1..S], temp1[1..S] );
}

max 操作跟min很类似，把 infinity改为 negative infinity，然后把 SIMD_MIN 换成 SIMD_MAX 就可以了

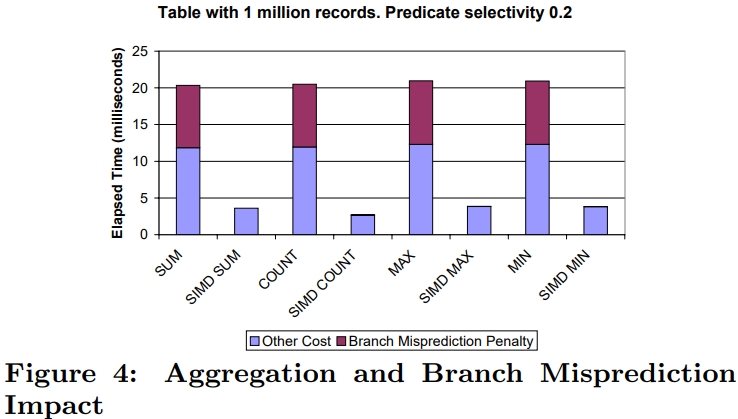
下面是原始聚合，以及SIMD聚合对比，使用的SQL就是普通的聚合+where
SELECT AGG(y) FROM R WHERE x_low < x < x_high
SIMD没有分支预测失败的开销，而普通的操作 40%时间消耗在了分支预测上，SIMD差不多是原始的 4倍

Index Structures

包含

  • 树结构索引
  • bitmap索引
  • hash索引

这里以树索引为列，树索引又细分为

  • ISAM
  • B+树
  • 多维索引 Quad tree
  • K-D-B tree
  • R-tree

每种树结构都有中间节点、叶子节点两种
在中间节点需要找到合适的子节点，而叶子节点只需要遍历就可以了

Internal Nodes

B+树的page大小一般跟系统的page一样，或者是其倍数，叶结点和中间节点都是 至少半满的
中间节点包含 n 个排序的key，指向 n + 1个 叶子节点
每个叶子节点有一个key(id)，指向row，也就是真实内容
论文中使用的key是32位的，对应变长的string，可以用定长算法将其修改为定长的
SIMD指定需要key和指针都是对其的
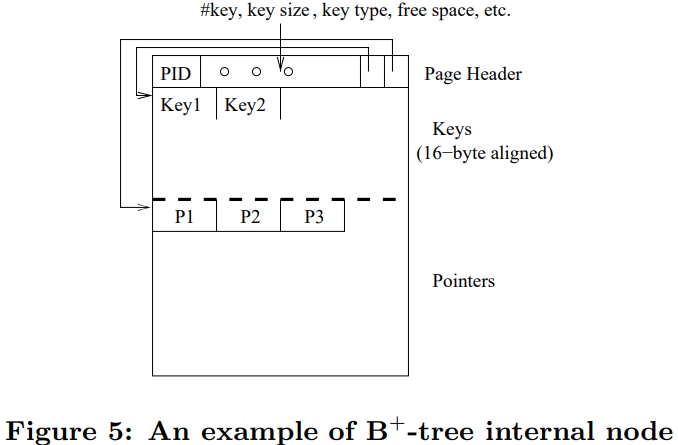B+ 树中间节点的这种特性，可以使用二分查找，但是二分查找使得预测失败接近 50%，导致性能下降

Naive SIMD Binary Search
SIMD版本的二分查找没有什么特别的

  • 首先是找到中间元素，这次是一次加载 4个元素
  • 然后跟目标比较，如果掩码是 4个0，则向左边继续查找
  • 如果全都是1，则往右边查找
  • 如果包含0 和1，说明找到了
  • 使用 SIMD bit vector 计算出结果
  • 原生的SIMD二分并没有消除分支，只是每次加载的元素更多了而已

Sequential Comparison with SIMD
这种是顺序扫描，在消除分支的情况下，顺序扫描是很快的
也就是从头扫到尾
另一种改进是比较当前结果是否大于 目标key，平均而言，这样可以节省一半的扫描时间

Hybrid Search
这是二分 + 顺序扫描的组合，对很大的元素来说，二分是对数时间，肯定是最优的
但是它有很多预测失败的场景，而顺序扫描在小数量的情况下表现得很好
所以结合这两者，设置 L = 64，然后对整个数组做分片，按照64位一个基本单位
然后先做二分，当定位到一个具体的分片时，就用顺序扫描

Experiments
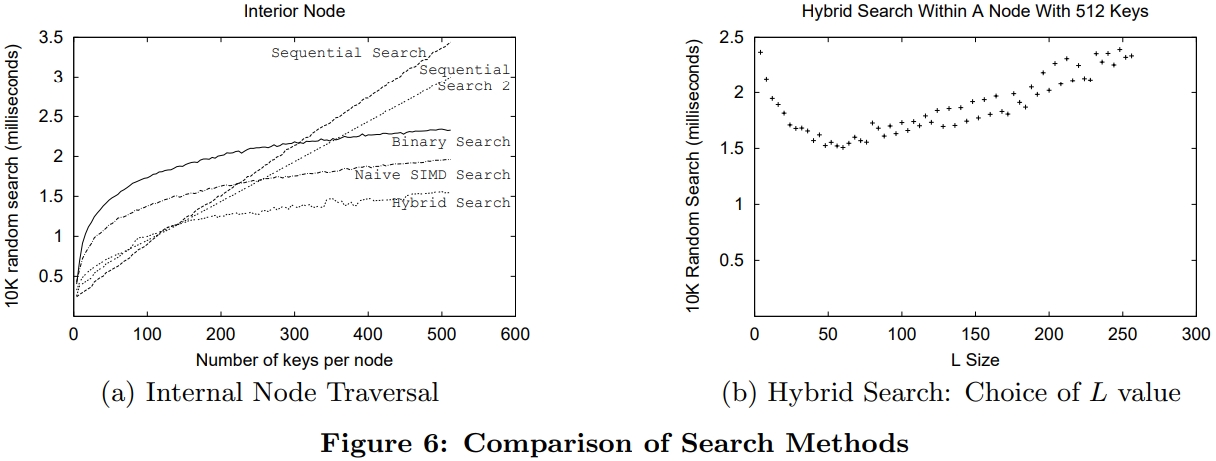
从测量结果看，当数量顺序扫描1、顺序扫描2在小数量的情况下表现的很好
而当数量超过 L(64)之后，就变成线性增加了，此时二分就更有优势了
SIMD版本二分比原始的二分更快，而hybird版本基本是最好的
可以得出结论，在元素很少时，比如 小于 L时，可以直接用顺序扫描
其他情况下就可以用 hybird版本

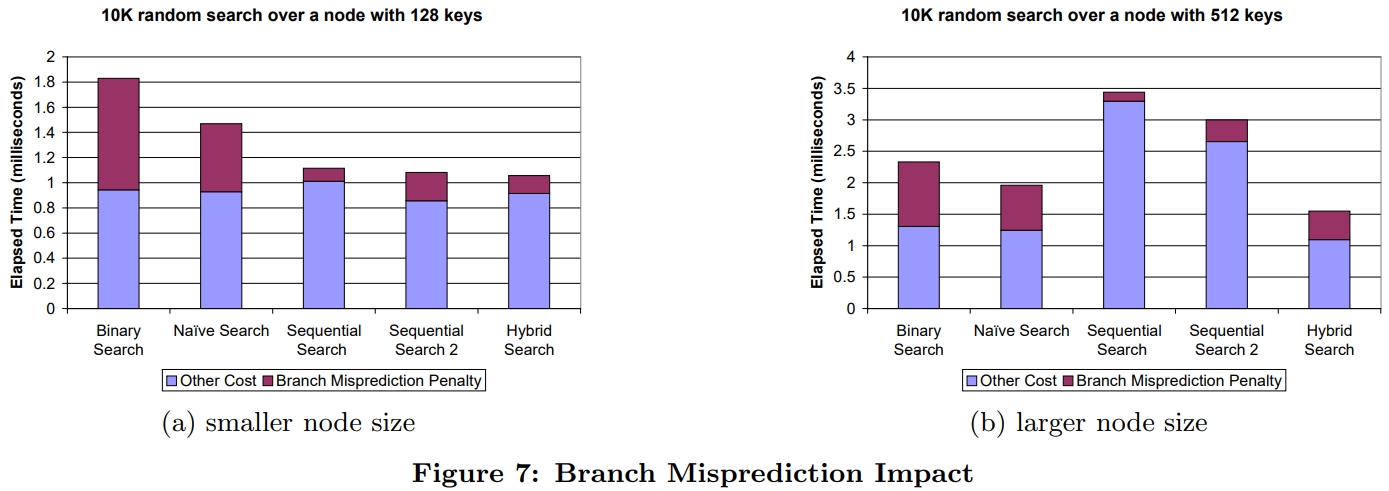
普通版本的二分其分支预测失败很高，所以其执行时间却是最长的，下图(a)
两个顺序版本的预测失败比率都很低，混合版本的预测失败比率也比较低
而当key变大时候，顺序扫描的时间就变得更长了(b)
SIMD版本比原始二分的预测失败略少一些，hybrid版本的预测失败是三个二分中最少的

Quad Trees and R-Trees
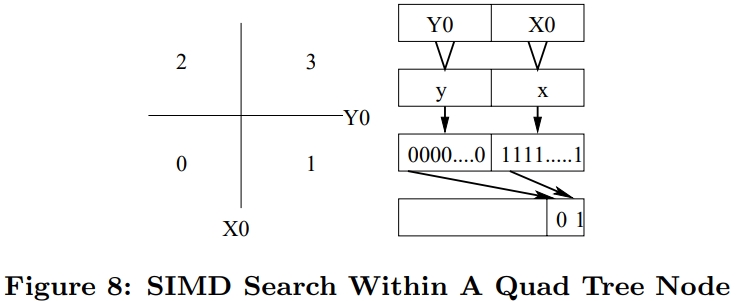
SIMD也可以用于空间搜索
四叉树，R树
对于R树，如果有S个维度，可以比较高维和低维，也就是两次就行了，而正常的需要比较 2S 次

Leaf Nodes

叶结点跟中间节点的设计是类似的，大部分的设计都可以参考
另外叶子节点可以顺序扫描，这样就不用保持有序了，对于增删改来说会更简单

对于多维索引中的叶子节点，一般是将每个维度存储到独立的数组中
SIMD指令在每个维度中比较 S个key，这样就得到了一个掩码的 S个元素，总体来说跟B+树设计比较类似

Overall Tree Performance

使用上述技术，实现了 一个 3级的B+树结构
包含 1KW个key，每个node为 4K大小，包含了 500个 32位的浮点数，以及一个32位的指针
使用混合搜索处理 中间节点，以及叶子节点

总体看有 10%的提升，加速效果不是很明显
因为还有其他的开销，比如cache miss的开销
增删改都会执行搜索，所以比之前更快

Join处理算法

nested loop join是最常用的处理方式，可以用来处理 等值、非等值的情况
有三种SIMD实现方式

  • Duplicate-outer，从outer表中找到一个key，然后复制S次，变成一个SIMD单元，然后遍历每个内部表，比较方式是之前介绍的那种，如果匹配了则放到结果集中
  • Duplicate-inner，从outer表中找4个key组成一个SIMD单元，然后遍历内部表，内部表的一个key复制4份组成另一个SIMD寄存器，然后比较这两个SIMD寄存器
  • Rotate-inner，从outer表中找4个key组成一个SIMD寄存器，再遍历内部表找4个key组成另一个寄存器，比较这两个寄存器S次，每比较一次，内部表的寄存器都做一次 rotate

在寄存器足够多(大于S个)的情况下，Rotate-inner 是性能最好的
预先计算外部表的SIMD寄存器，做预rotate，并针对内部表做 4个比较，此时不需要rotate
至于连接比较的方式，也可以通过 SIMD 指令集做转换

四个SQL

1
2
3
4
5
6
7

Q1: SELECT ... FROM R, S WHERE R.Key = S.Key

Q2: SELECT ... FROM R, S WHERE R.Key = S.Key

Q3: SELECT ... FROM R, S WHERE R.Key < S.Key < 1.01 * R.Key

Q4: SELECT ... FROM R, S WHERE R.Key < S.Key < R.Key + 5

第一个比较是基于整数的，其他都是浮点数
外表是10^6个tuple，内标是10^4 个tuple

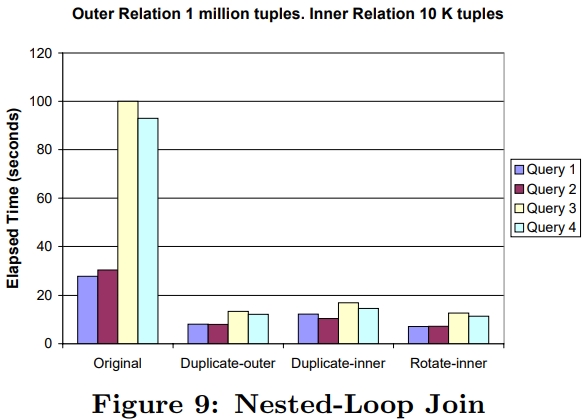
原始nested-loop join 和三个SIMD版本比较如下：

  • 三个SIMD版本比原始版本都要快很多
  • duplicate-inner比其他两个SIMD略慢一些，因为要执行 10^6 * 10^4 / 4，这么多次
  • 而duplicate-outer需要执行 10^6次，所以略快
  • 而rotate-inner是最快的
  • 查询1、2有4倍提升，查询3、4有9倍提升

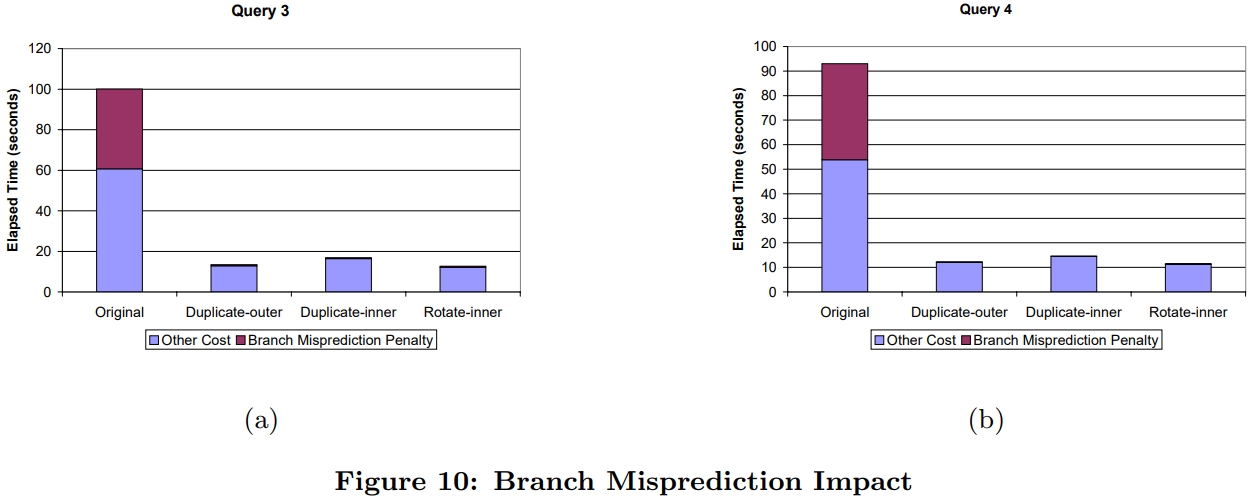
下面是查询3、查询4的分支预测失败开销
可以看到原始版本有40%的时间花在了分支开销上，而 3个SIMD版本几乎都没有
论文中还提到了一个有意思的现象，奔腾4 CPU的普通浮点计算时间，比SIMD浮点运算要慢一些

Optimizing for the Common Case

由于join的选择率大多数情况下是很小的，所以像

1

if(V != 0)

这样的比较还是值得的

假设选择率很小，比如0.0001
实现一个函数映射，将32bit key映射为16位的、8位的、4位的
当然这里可能会产生冲突
值更小就更适合放到cache中
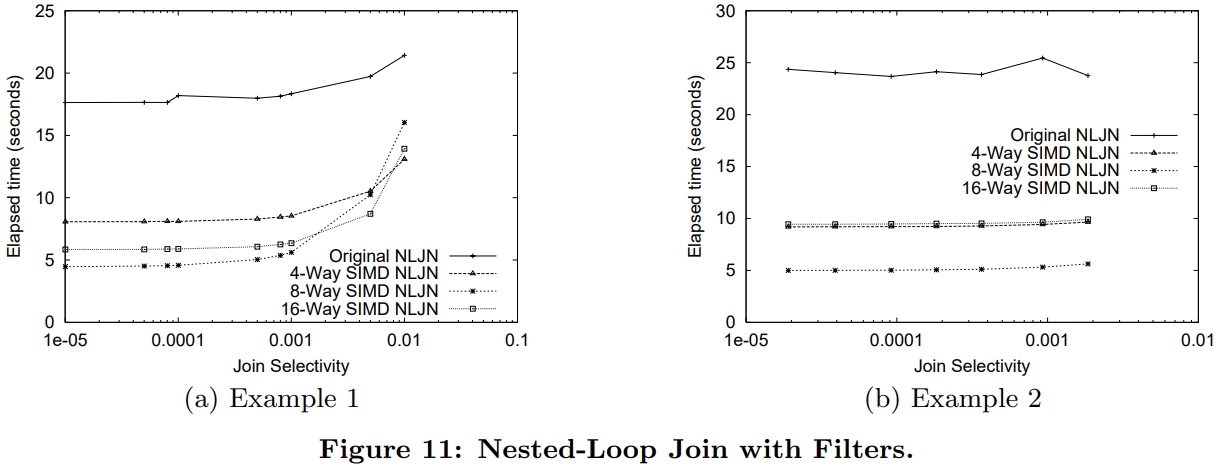
总体上看 8路的是最好的，但随着选择率的提升，4、8、16都有下降
这时候可以依靠优化器来选择合适的方式

另一个例子，假设有两个表

  • wants(Client,Facility)
  • supplies(Location, Facility)

SQL如下：

1
2
3
4
5
6
7

SELECT Client, Location
FROM wants C, supplies S
WHERE (SELECT Facility FROM supplies G
		WHERE G.Location = S.Location)
		Contains
		(SELECT Facility FROM wants H
		WHERE H.Client = C.Client)

假设客户和供应商很多，而facilities表很小，如果facilities表数量小于 d
那么可以用 d 个bit来表示facilities表，或者客户、供应商可用的facilities
这时候就得到了两个新表

  • wants(Client,bitmap)
  • supplies(Location,bitmap)

对应的SQL可以写成：

1
2
3

SELECT Client, Location
FROM wants C, supplies S
WHERE (C.bitmap & S.bitmap = C.bitmap)

性能对比如 figure 11

参考