原文 https://15721.courses.cs.cmu.edu/spring2023/papers/04-olapindexes/p355-chan.pdf

背景

大多数的索引优化是针对 OLTP 场景的，OLAP 索引的较少
论文提出了对 bitmap 索引的设计的一个指导性框架
为物理数据库设计 bitmap 索引时提供一份直到方案

  • 时间最优的 bitmap 索引
  • 空间最优的 bitmap 索引
  • 空间时间权衡最优的 bitmap 索引
  • 给定磁盘空间限制下的时间最优 bitmap 索引

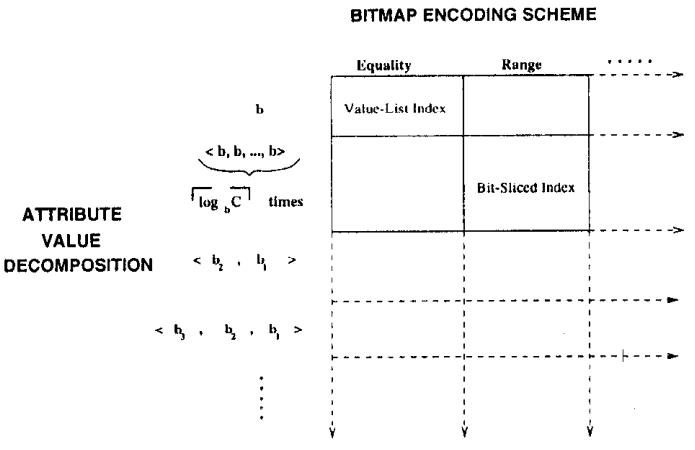
在一列属性上创建 bitmap 索引，这列上一共有9种不同的值
对应的 bitmap索引有 8 - 0 一共 9列，相当于是 9个 Value-List Index
每个 list 对应一个值，比如第二行，(a)第二行是2，对应的(b)，第二行的B2 是1，其他都是0 第六行也是2，所以(b) 中 B2 这个list，第6 个bit也被设置为了 1

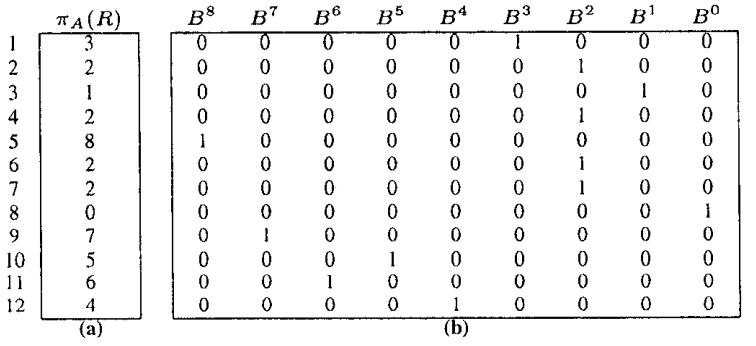
Figure 1: Example of a Value-List Index. (a) Projection of indexed attribute values with duplicates preserved. (b) Value-List Index.

对于一个带有谓词的查询，传统的数据库一般是三种方案：

  • 全表scan
  • 索引scan(使用低选择率的)，然后跟随一个部分scan，过滤掉不符合的tuple
  • 对每个选择的谓词都做scan，然后 merge他们的结果

bitmap 在带有压缩场景下，使用第三种，再配合硬件，效率是最高的

论文的贡献

  • 提出了一种设计 bitmap 的通用框架，不光对现有提案有帮助，对其他方案也有帮助
  • 提出了四种时空权衡：空间优化、基于空间限制下的时间优化、时间优化、时空权衡
  • 对 bitmap 压缩的的研究
  • buffer 对时空权衡的影响
  • 更有效的bitmap 索引求值算法，减少了50% 的操作，并减少了一次bitmap scan


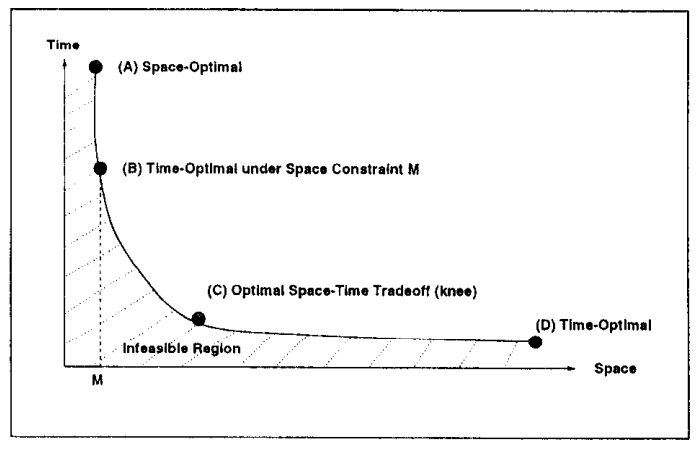
Figure 2: Space-Time Tradeoff Issues

设计

属性值分解，跟图1 的属性值一样，但是这里做了分解，将一个 bitmap分解为 <3,3> 结构
原先需要 bitmap 数量从 9 减少到 6
B2-2，B1-2，B0-2分别表示：3 * 2、3 * 1、3 * 0
B2-1，B1-1，B0-1分别表示：2、1、0 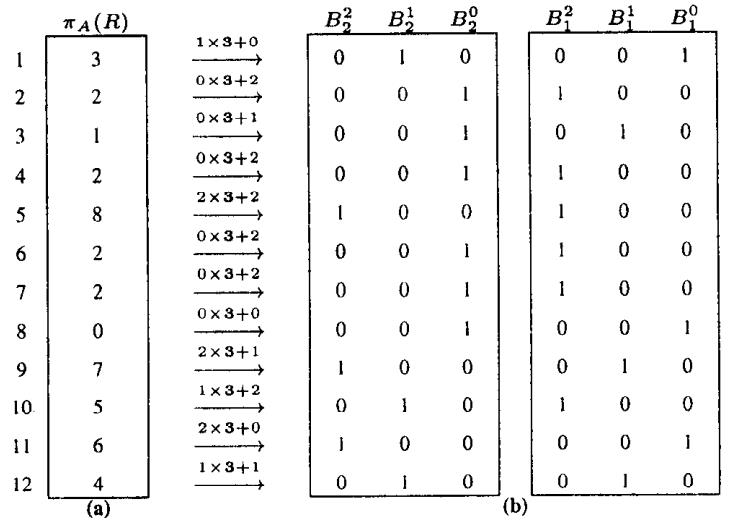Figure 3: Example of a 2-Component Value-List Index (a) Projection of indexed attribute values with duplicates preserved. (b) Base-< 3,3 > Value-List Index.

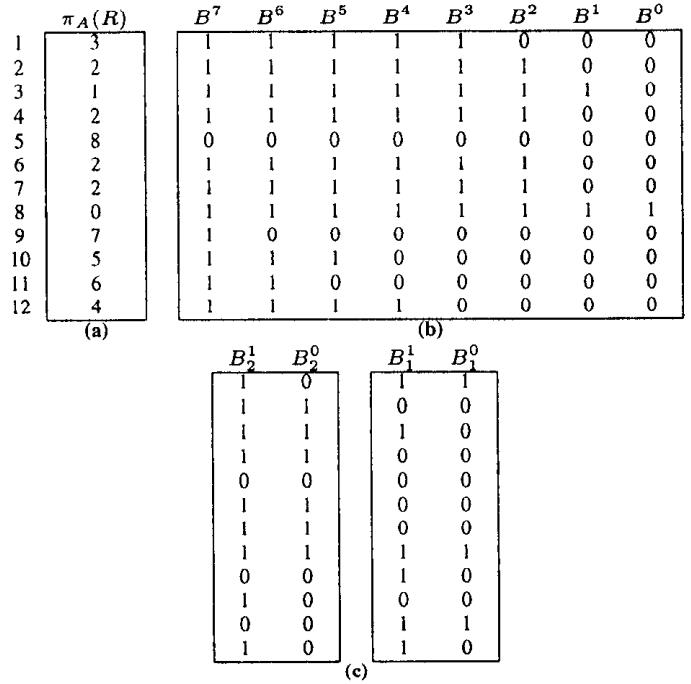Figure 4: Examples of Range-Encoded Bitmap Indexes. (a) Projection of indexed attribute values with duplicates preserved. (b) Single Component, Base-9 Range-Encoded Bitmap Index. (c) Base- < 3,3 > Range-Encoded Bitmap Index.

图5显示了用于选择查询的索引的二维设计空间，有两种现有的备选方案

  • Value-List索引
  • bit - slicing索引

分类如下所示
Value-List索引是最简单的索引，也是最常实现的索引，它只有一个组件，并且是等号编码的
位切片索引有一个统一的基数，并且是范围编码的

算法改进

Algorithm RangeEval-Opt是一种优化的评估算法，它避免了中间的等值谓词评估，通过仅基于以下三个等式对每个范围查询进行“5”谓词的评估：

  • A < v 相当于 A <= v - 1，
  • A > v 相当于 A >= v，
  • A = v 相当于 A >= v - 1，并且不需要等值谓词评估
    Figure 6: Algorithms RangeEval and RangeEval-Opt.

图7比较了使用3个组件的基数为10的索引来评估谓词“A = 864”的两个算法

  • Algorithm RangeEval-Opt更高效，它只需要4个位图操作和5个位图扫描
  • 而Algorithm RangeEval则需要10个位图操作和6个位图扫描
  • 此外，Algorithm RangeEval-Opt的高效处理仅需要为一个位图（中间/最终结果）进行缓冲
  • 而Algorithm RangeEval的高效处理需要为两个位图（BEQ和BGT/BLT）进行缓冲
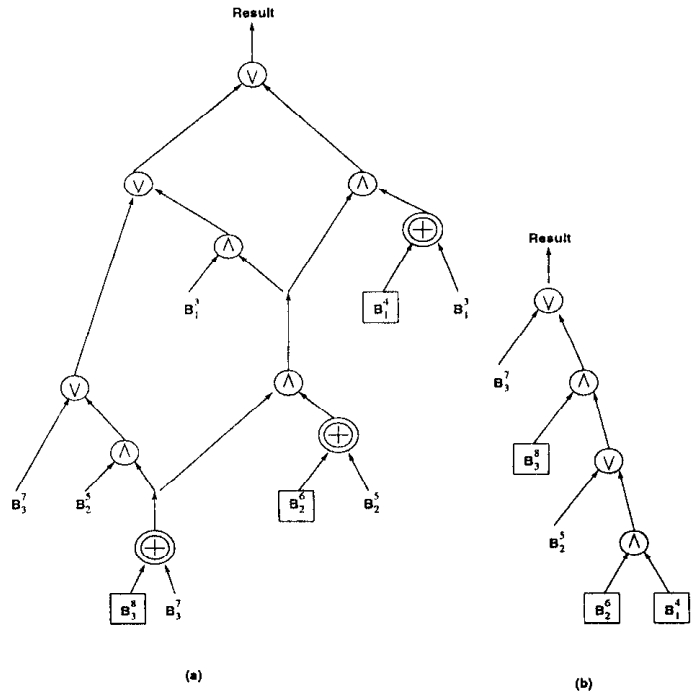
    Figure 7: Comparison of Evaluation Strategies for Selection Predicate “A 5 864” using a 3-Component, Base-10 Range-Encoded Bitmap Index. (a) Algorithm RangeEval. (b) Algorithm RangeEval-Opt.

Table 1显示了评估算法在位图操作和扫描数量方面的最坏情况性能分析

  • 对于Algorithm RangeEval，由于每个范围谓词评估都需要进行等值谓词评估（对于BEQ位图），范围谓词评估的位图操作数量至少是“=”谓词评估的两倍
  • 通过使用更直接的评估策略，Algorithm RangeEval-Opt将范围谓词评估的位图操作数量减少了约一半；范围谓词的位图扫描数量减少了一个
  • 两个算法在等值谓词评估方面具有相同的成本。对于两种评估算法，最坏情况发生在0 < w2 < b; - 1, 1 < i 5 n的情况下，这也对应了最有可能的情况 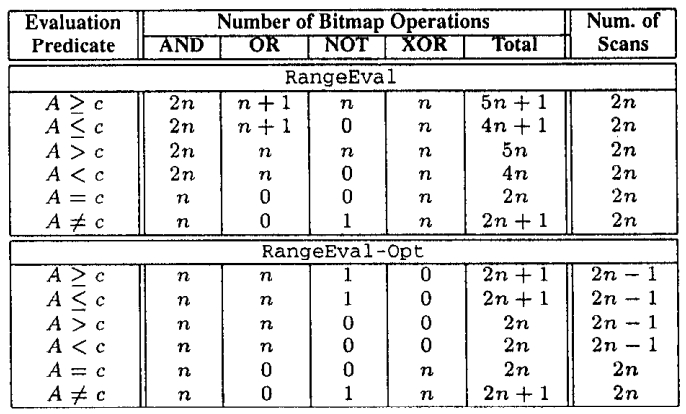Table 1: Worst Case Analysis of Evaluation Algorithms; n is the number of index components

两种算法的性能对比
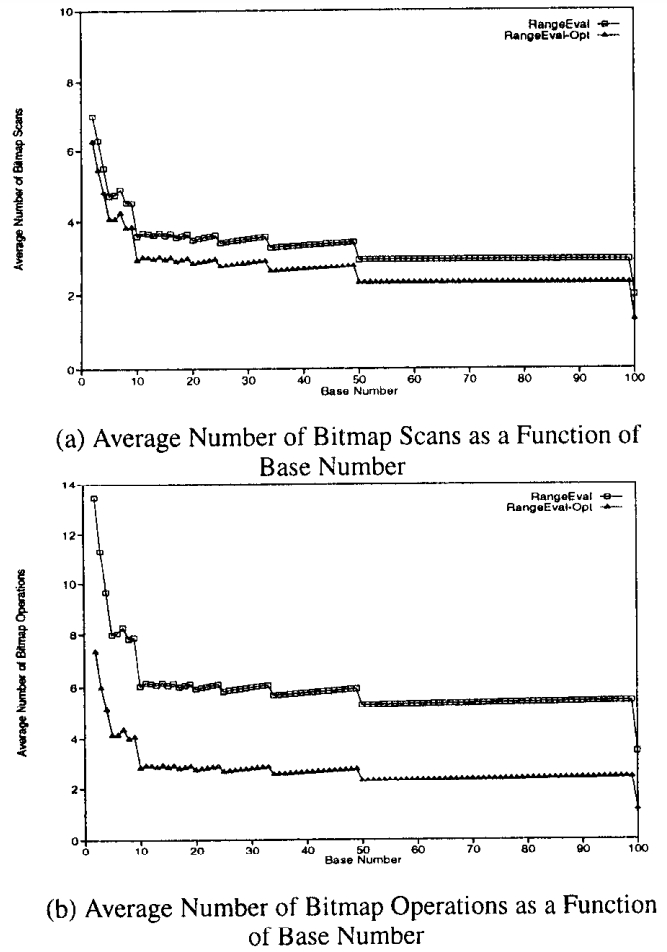Figure 8: RangeEval vs RangeEval-Opt for Uniform Base Range-Encoded Bitmap Indexes, C = 100.

优化

时空权衡的两个指标

  • 空间指标是以存储的位图数量为单位。
  • 时间指标是以选择查询评估的预期位图扫描次数为单位

时间指标仅包括I/O成本（即位图扫描次数），不包括CPU成本（即位图操作次数），因为查询评估的位图扫描次数和位图操作次数是相关的

范围编码，比等值编码，提供了更好的 时空权衡

在不同的基数情况下，范围编码，比等值编码提供了更好的时空权衡
所以后续所有的优化都是基于范围编码来的

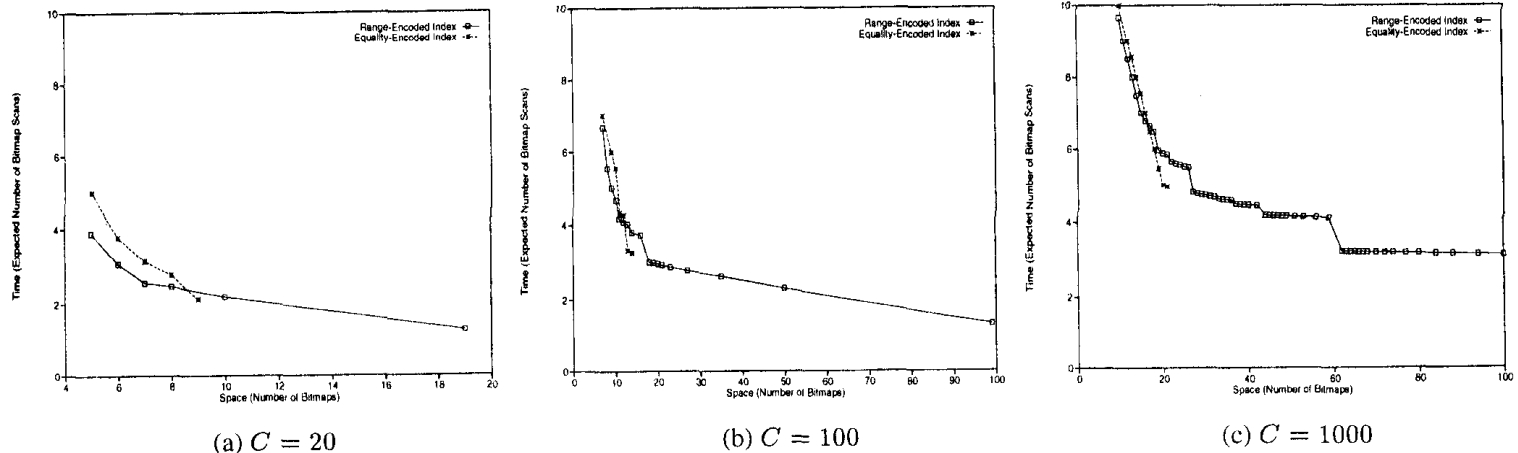
Figure 9: Comparison of Space-Time Tradeoff of Range- and Equality-Encoded Bitmap Indexes

图10比较了三类索引的空间-时间权衡图

  • 空间最优索引类
  • 时间最优索引类
  • 全部索引类

其中C = 1000；对于其他C值，可以得到类似的结果
空间最优（或时间最优）索引的图形最多由[log2(C)]个点组成，其中每个点对应于一个n组分的空间最优（或时间最优）索引
1 ≤ n ≤ [log2(C)]。请注意，由于空间最优索引通常不唯一
图中的每个点对应于在具有相同组分数的所有空间效率相等的索引中最具时间效率的索引
图10显示了空间最优索引的权衡图对所有索引的良好近似。特别地，空间最优索引图上的点集是全部索引图上的点集的子集 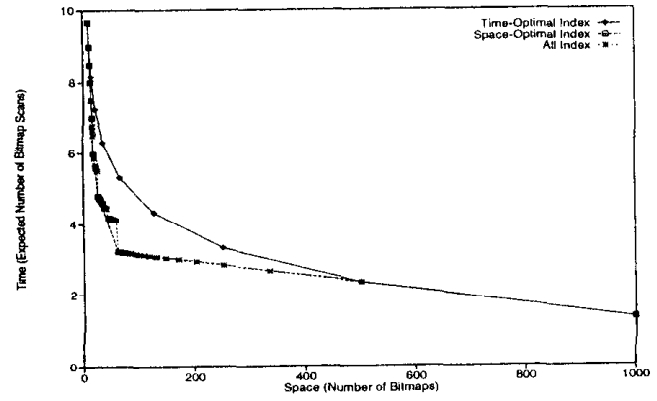Figure 10: Space-Time Tradeoff of Bitmap Indexes, C = 1000.

图11展示了与图10相同的空间最优权衡图
但是每个点都标有相应空间最优索引的组件数 空间最优索引的空间-时间权衡图的“膝部”对应于一个2组分索引
实验中一直保持一致。因此将“膝部”索引定义为最具时间效率的2组分空间最优索引
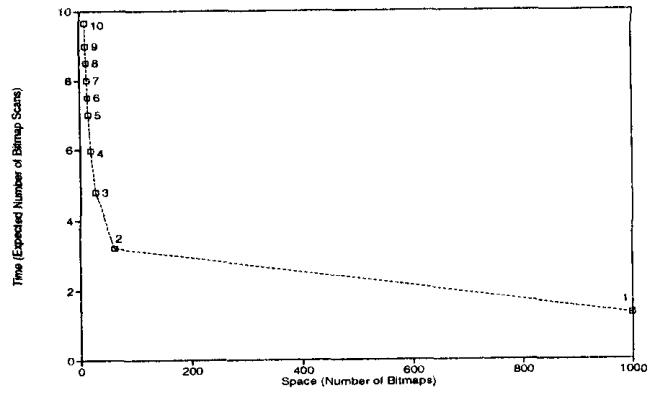Figure II: Space-Time Tradeoff of Space-Optimal Bitmap Indexes, C = 1000.

图13展示了两种情况，以说明解决方案索引的组件数的上下界；所示空间-时间权衡图上的每个点都标有相应索引的组件数 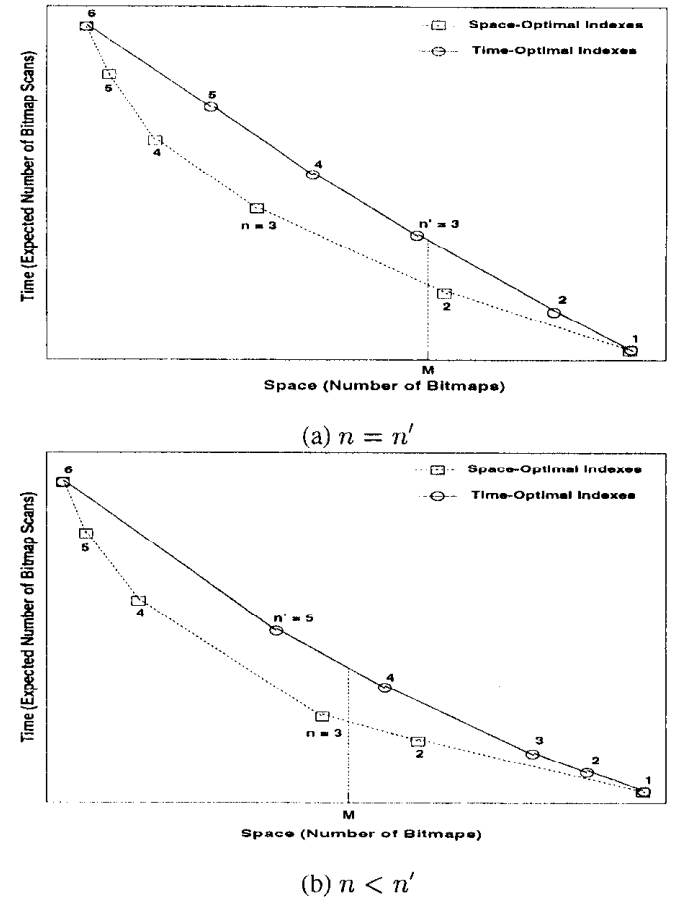Figure 13: Bounds on Number of Components of Solution Index in Algorithm TimeOptAlg.

算法的时间复杂度由步骤4中定义的候选索引集合Z的大小确定。由于我们需要枚举每个值k，其中n ≤ k < n’，所有可能的k组分索引，使得n’’ ≤ bi ≤ C，并且Cfzl(bi - 1) ≤ M。图14显示了Z的大小作为M的函数，其中C = 1000
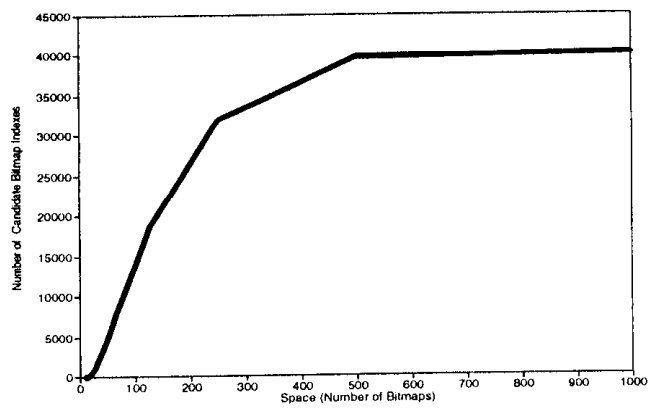Figure 14: Size of Set of Candidate Bitmap Indexes, 2, as a Function of the Space Constraint A4 for C = 1000.

为了避免在最优方法中的耗时穷举搜索（步骤4和5），论文提出了一种启发式方法（图12中的算法TimeOptHeur）以找到一个近似最优解
这种启发式方法几乎是最优的，最优索引至少被选择了97%的时间
主要思想是首先选择一个满足空间约束的“种子”索引，然后通过调整其基数来提高种子索引的时间效率

表2展示了启发式方法在不同属性基数值下的有效性
第二列显示了启发式方法选择的解决方案中与相应属性基数值最优解的百分比，在最优解和启发式方法产生不同解决方案的情况下
第三列显示了它们所选索引的预期位图扫描次数的最大差异。结果表明，所提出的启发式方法接近最优解
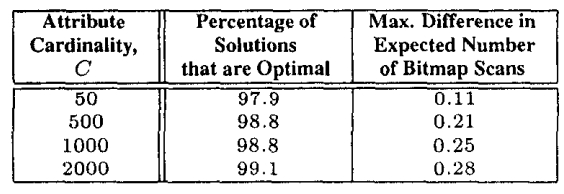Table 2: Effectiveness of Heuristic Approach to Select TimeOptimal Bitmap Index under Space Constraint.

三种存储方案

  • 位图级存储（BS）：每个位图单独存储在一个包含N个位的位图文件中。因此，位图索引存储在n个N位的位图文件中。
  • 分量级存储（CS）：每个索引分量按行主序存储在一个包含（N x ni）个位的位图文件中，1 < i < lc。因此，位图索引存储在k个位图文件中。
  • 索引级存储（IS）：整个索引按行主序存储在一个包含Nn个位的位图文件中

实验研究使用了从TPC-D基准测试[4]中提取的两个数据集：数据集1用于小属性基数，数据集2用于大属性基数
表3显示了我们实验数据的主要特征。为了限制每个数据集的实验数量
空时权衡比较仅限于空间最优索引类（作为索引分量数量n的函数），其中n的取值范围从1到6
Table 3: Characteristics of TPC-D Benchmark Data used in Experiments

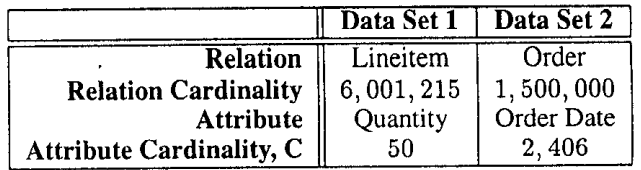
表4比较了两个数据集中三种存储方案的可压缩性。对于每个n分量索引I和每个压缩存储方案S（其中1 ≤ n ≤ 6，S ∈ {CBS，cCS，cIS}）
我们计算在S下的I大小与在BS下的I大小之比。对于两个数据集，结果表明CS索引提供了最佳的压缩效果。
在查询评估成本方面，BS索引每个索引分量最多需要扫描2个位图文件。另一方面，CS索引和IS索引都需要扫描所有位图文件
此外，它们还需要额外的CPU开销来从分量位图文件中提取每个相关位图的位（这些文件是按行主序存储的）
因此，我们预计CBS索引比cCS索引和cIS索引更高效
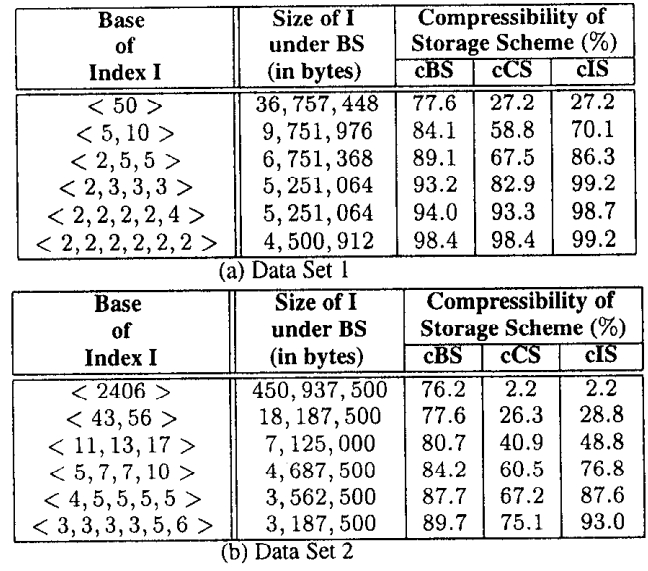Table 4: Comparison of Compressibility of Different Storage Schemes.

图16(a)将索引的时间效率与索引组件数量进行了比较
BS和CBS索引明显优于cCS索引；特别是对于cCS索引，超过70%的总评估时间是由于位图解压缩。cCS索引的解压缩成本通常随着位图组件数量的增加而增加 图16(b)将索引的空间效率与索引组件数量进行了比较。有两个主要观察结果

  • 首先，正如我们已经从表4中了解到的那样，cCS索引是最具空间效率的
  • 其次，结果显示，随着组件数量的增加，位图压缩的有效性减弱。这可以通过以下事实来解释：位图的数量是组件数量的递减函数

当一个索引从一个组件分解为两个组件时，会有显著的空间减少。因此，一旦索引被分解（即n ≥ 2），就相对于空间减少而言，位图压缩的收益仅仅是微不足道的
图16(c)比较了索引的空间-时间权衡。结果显示，BS索引和CBS索引具有可比较的空间-时间权衡，优于cCS索引
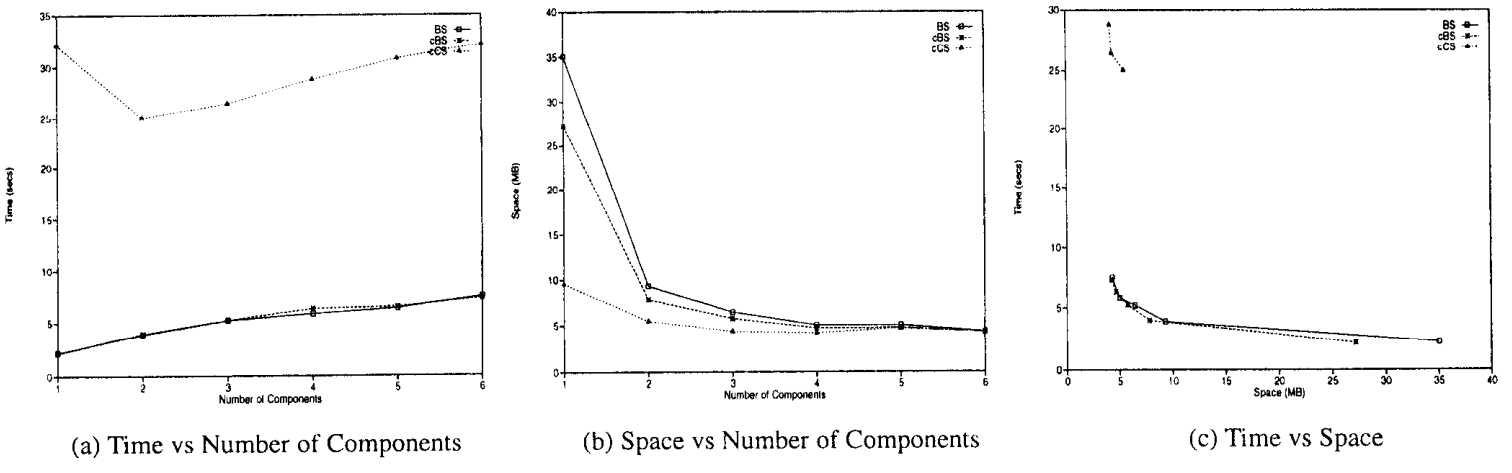Figure 16: Comparison of Space-Time Tradeoff of Compressed Bitmap Indexes under Different Storage Schemes for Data Set 1.

Figure 17展示了基于最佳位图缓冲策略的索引在缓冲位图数量m变化时的空间-时间权衡情况，其中C = 1000。如预期所示，随着m的增加，空间-时间权衡得到改善
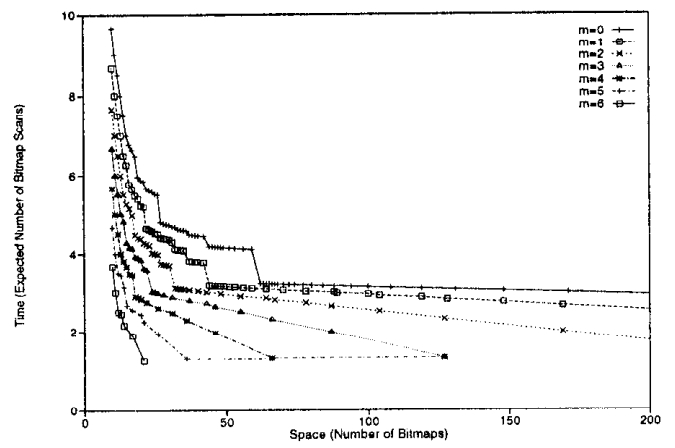Figure 17: Space-Time Tradeoff as a Function of the Number of Buffered Bitmaps m, C = 1000.