原文 https://15721.courses.cs.cmu.edu/spring2023/papers/04-olapindexes/rao-vldb97.pdf

背景

现代系统是从面向磁盘，转向了面向主内存的数据库
而从 1986年开始，CPU的增速是 60%一年，内存只有10%，两者差距越来越大
这就导致 cache miss 增加了两个数量级

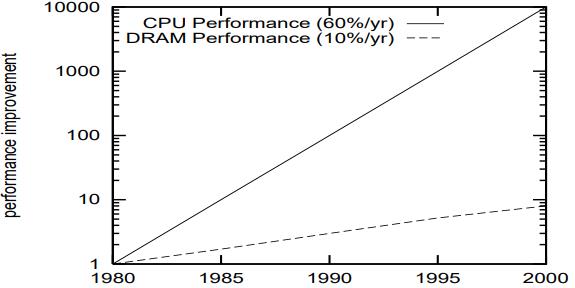
Figure 1: Processor-memory performance imbalance

另一个点是 OLAP 主要还是读场景，论文主要关注的点还是 OLAP 场景
而索引技术在 OLTP 的主内存数据库中仍然有很大用处，论文就提出了一个新的索引技术
Cache-Sensitive Search Trees，CSS-trees
这种技术的好处是做到了空间、时间的权衡，都是比较优秀的
对比现有的各种技术

  • array binary search
  • T tree、enhanced B+ tree
  • hash indexes、interpolation search

有些技术的空间占用很小，如 二分查找不占空间，但是时间占用挺大的(cache miss)
有些时间上很好，但是空间占用很大如 hash indexes
CSS tree在空间和时间上比 增强 B树、T树 更好
所以对主内存索引来说，要关注的就是亮点

  • 时间
  • 空间
    Figure 2: Space/time Tradeoffs

论文是在主内存数据库基础上，提出了针对 cache 有效性改进的一些算法
并和现有算法的评估

Cache Sensitive Search Trees

现有的各种索引问题

  • Array Binary Search，如果排序的数组远大于cache，那么最坏的情况是，有多少次比较，就有多少次 cache miss
  • T tree，将连续排序的数据放在一起了，看上去是缓存敏感的实际跟二分类似，只有min、max用到了，cache miss仍然有，比二分好不了多少
  • B tree，虽然是面向磁盘的，但他的cache有效性比 T树更好，因为有多个子节点指针，cache中可以满足多个比较条件
  • 增强B tree，在OLAP 场景的优化，节点时全满的，另外节点大小匹配了cache line
  • hash，这也是缓存敏感的，但hash不保证顺序还需要额外一个有序列表，另外hash需要非常大的空间，否则冲突链可能会很长

CSS 树结构如下，假设 m = 4，也就是一个 node 包含 4个元素

  • 这种结构有点像 B树 + 树堆的组合，一棵树有 N + 1 个子节点
  • 但是这些子节点并不是用指针来指向的，而是用数组下标
  • 这是在一个排序数组之上，用了一个额外的辅助数组实现的
  • 它的叶子节点位置，跟实际排序数组的位置正好是相反的，类似一个满二叉树的结构
  • 31-55，56-80是左子树的叶结点，在排序数组中对应的 后半部分
  • 16-20，21-25，26-30 对应的是排序数组的左半部分
  • 一个内部节点b，其子节点编号为 b(m + 1) + 1 – b(m + 1) + (m + 1)
    Figure 3: Layout of a full CSS-tree

更清晰的结构如下
$O(log{m+1}N)$， CSS 树的比较次数
$O(log{2}N)$， 二分的比较次数
差别是 m + 1 和 2

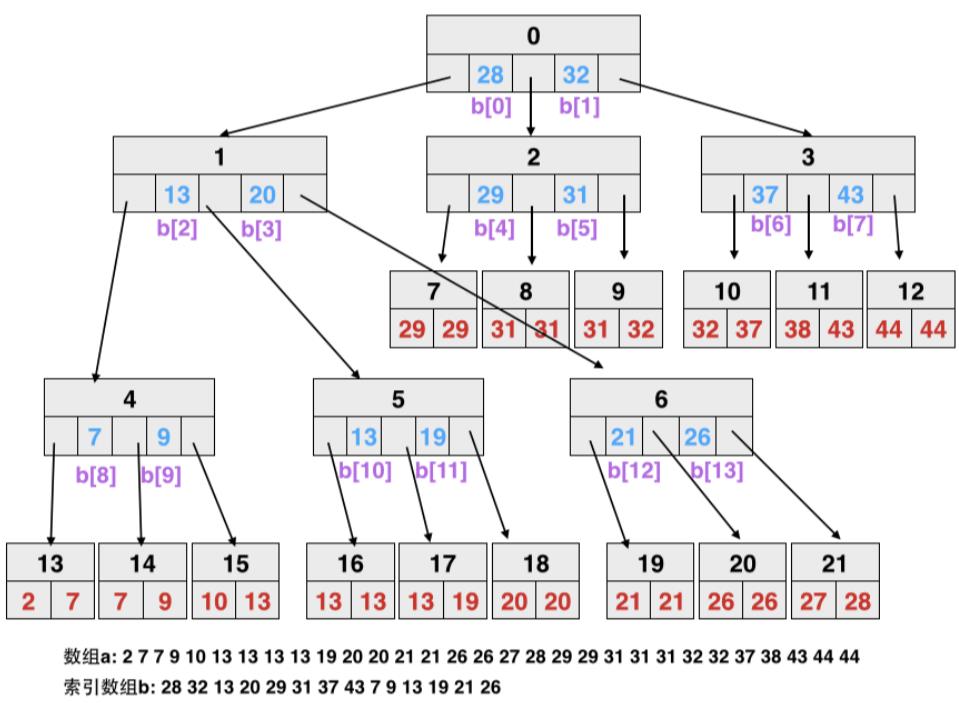
CSS tree 的构建

  • 首先将排序数组逻辑上分为两部分，part-1，part-2
  • 然后建立目录到 排序数组的映射
  • 从最后一个内部开始处理，它指向的是part-1的最大值
  • 需要注意的是，对于part-1部分，最后的叶结点其祖先节点，其值可能不完整
  • 比如下图的节点11，其祖先节点就不完整，这时候，叶结点不完整的部分，直接填充最大值就行了
  • 也就是part-1部分，最后一部分可能有很多重复的值，算法需要特殊处理一下
  • 好处是不用考虑数组下标越界问题

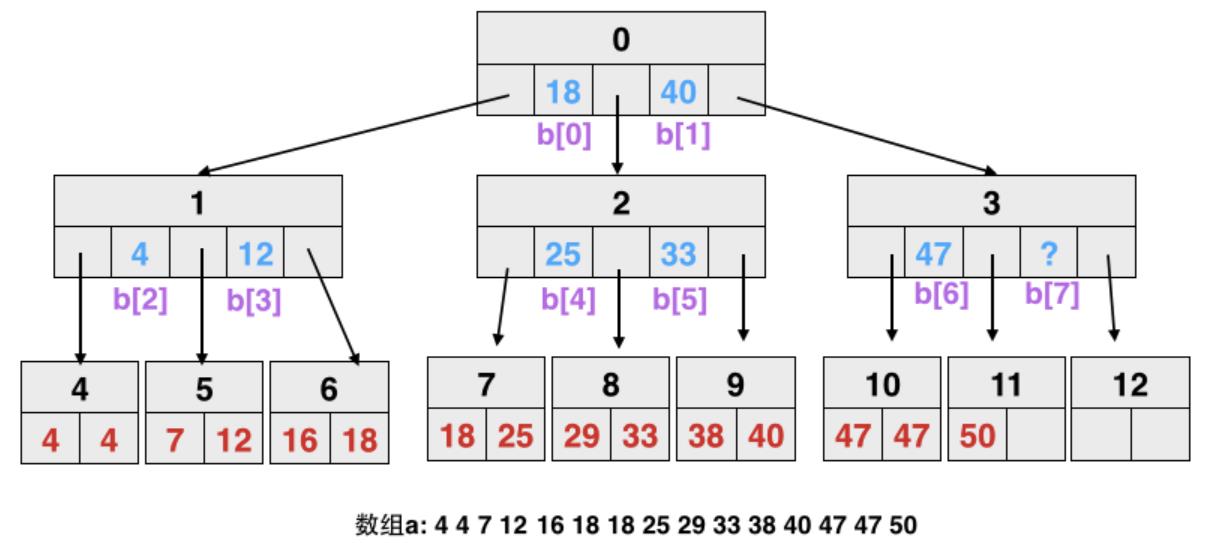
CSS tree 的搜索

  • 跟 B树 的搜索类似，先从根节点开始，然后在一个 node 内做二分
  • 这样就可以定位到子节点了，如果子节点也是内部节点继续二分定位
  • 当找到叶子节点了，继续分为定位，如果发现重复的，那就是 最左边的值

Level CSS-Trees

  • 当m取8的时候，在非叶子节点中的二分搜索是下面这样的
  • 一个节点会有9个branch。其中的7个需要比较3次，而2个需要4次
  • 为了使得每个branch都比较一样多的次数，建议当m = 2^k时，只使用其中的m-1个存储索引
  • 这样的实现就叫作Level CSS-Trees
  • 好处是：搜索的时间可以稍微减少一些，缺点是：存储索引的空间增大了 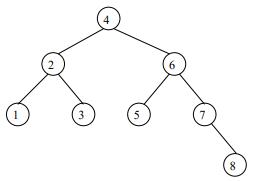Figure 4: Node with 8 keys

实验

时间分析

  • 分支因子、层的数量、内节点的比较次数、叶节点比较次数
  • 以及移动的次数，cache miss(node size 大于/小于 cache line情况)
  • 当 node size > cache line时，CSS tree的cache miss 是最少的 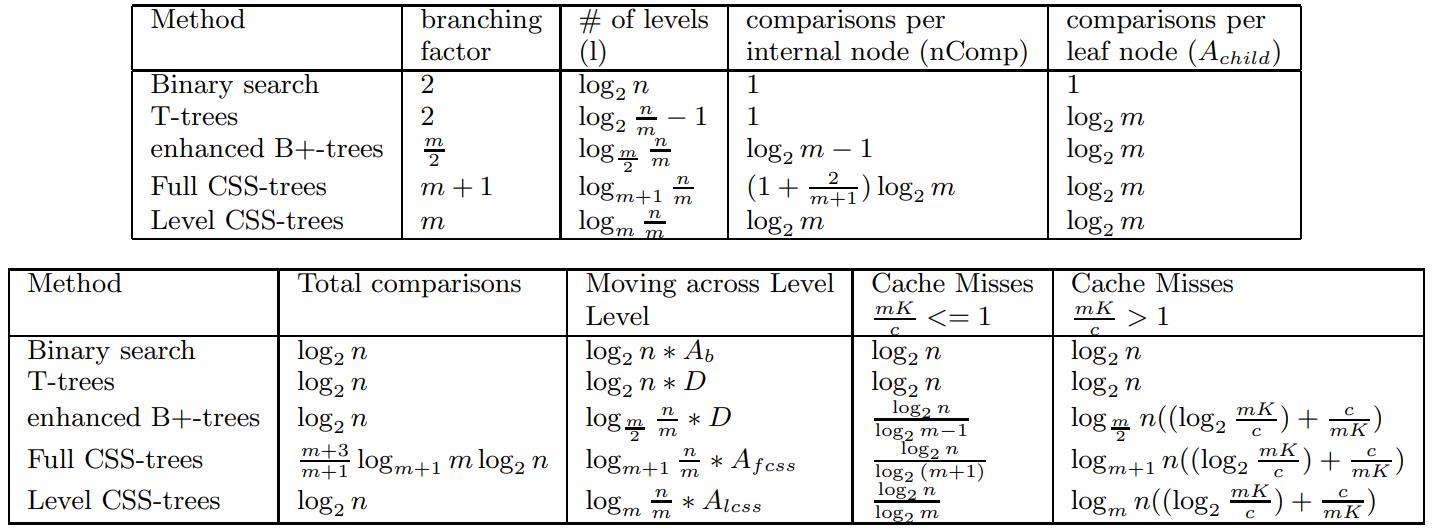Table 1: Time analysis

空间分析

  • Space (indirect)，说明这个空间是可以重排列的
  • Space (direct)，说明这个需求的空间不能重排列
    Table 2: Space analysis

比较各个算法的 build 时间，插值搜索是最差的
CSS tree 可以在 1秒内构建 2500W 个key，因为可以考虑周期重建索引
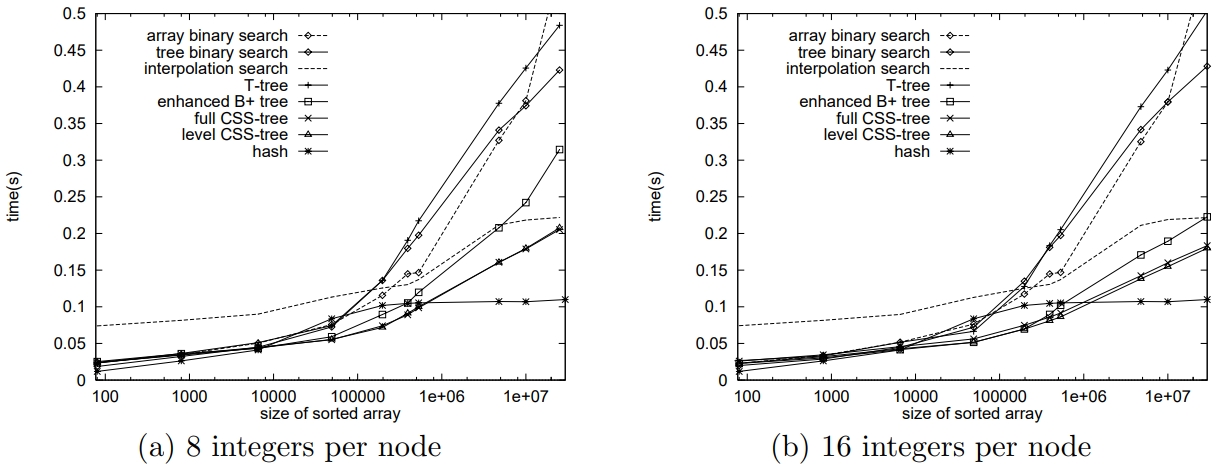Figure 5: Varying array size, Ultra Sparc II

比较访问时间，以及 cache miss 次数
从过去的报告看， T 树 比 二分查找和 B 树更好，这是因为报告太久远了，CPU和内存差别不是那么大
论文中显示 T 树的结果很不好
B 树比 CSS树 大约慢了 50%，这是 cache miss 导致的
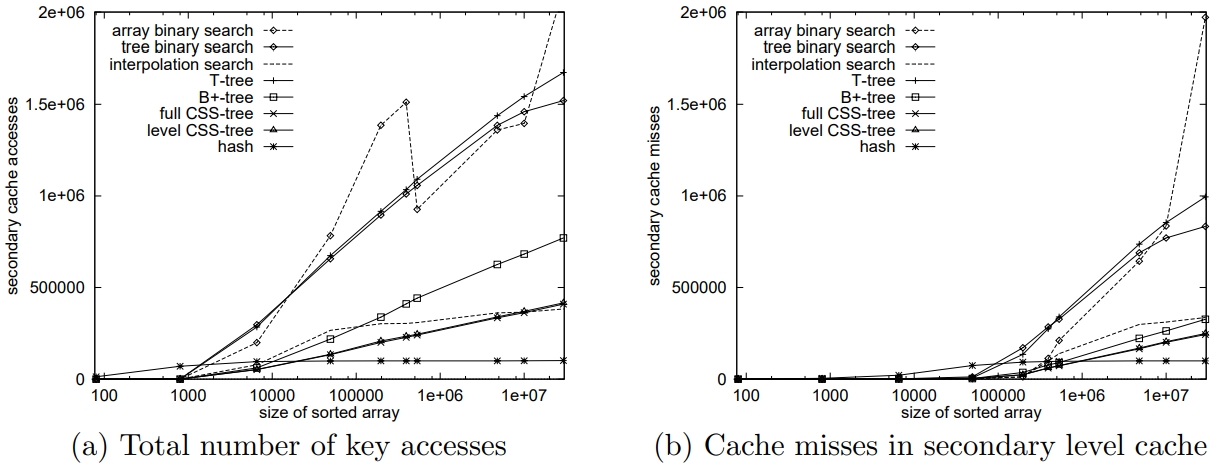Figure 6: Ultra Sparc II, 16 integers per node

下面是固定排序数组的大小，将每个算法的 node 设置为可变的
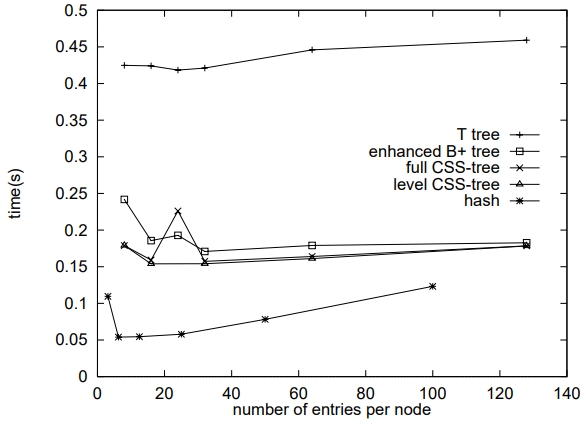Figure 7: Varying node size, 10 million keys

CSS tree 可以将搜索时间 减少为 二分查找的 1/3
而只需要一些额外的空间
对比了 CSS tree 和增强 B树 的cache miss，随着 CPU 和内存的差距越来越大
5年后，其 cache miss 可能就是 8(b) 的结果了
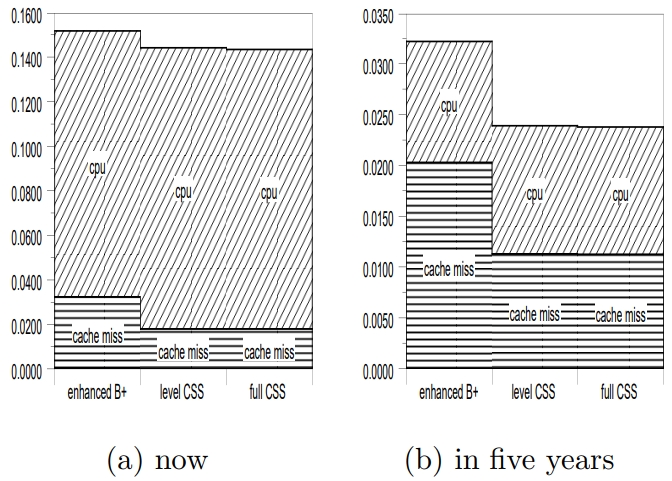Figure 8: Time breakdown (16 integers per node)

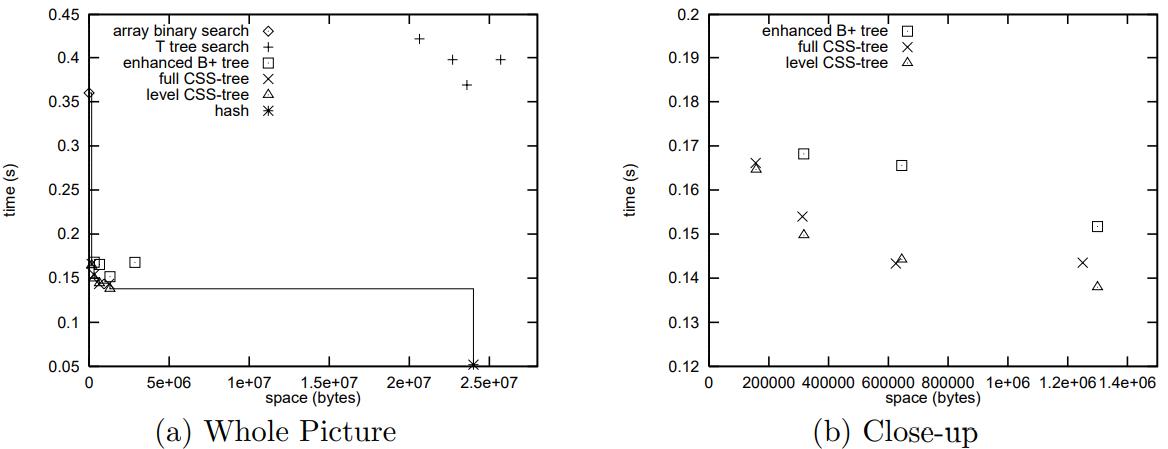
图9显示了五年内B+树和css树之间预计的空间/时间权衡
最优的css树比最优的增强B+树快近30%
在极限情况下，如果缓存丢失代价大于总代价，css -树可以比增强的快50%
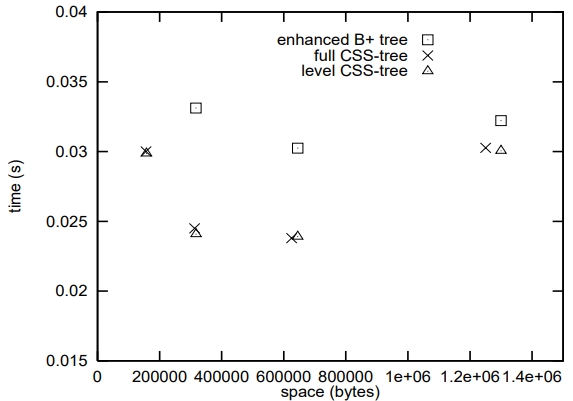Figure 9: Space/time Tradeoffs (in five years)

参考