原文 https://15721.courses.cs.cmu.edu/spring2023/papers/04-olapindexes/li-sigmod2013.pdf

背景

针对主内存数据库场景，scan 是一个非常重要的操作
为了让 scan 的速度尽可能接近 CPU 的处理速度，现有技术使用 SIMD加速，但这也有一些问题

  • 比如32 bit 的打包到 128bit 的SIMD 寄存器中，如果是 9bit压缩，意味着 32- 9 = 23bit需要做无畏的填充
  • 将 9bit 扩展为 32bit 也需要浪费额外的性能来处理

论文提出了的技术，单个处理器内部也有很大的并行度，可以并行计算多个 bit
论文提出了 BitWeaving 技术，可以利用 SIMD 的word带宽，包含两个版本

  • BitWeaving/V
    • bit级别列数据组织，打包到处理器words宽长度，再放到连续的内存中做scan 用
    • 谓词计算转为对这些bit 做逻辑计算
    • 方便做早期谓词裁剪，只需要计算每个列的重要几个bit 就可以skip 了
    • 产出的 bit 向量还可以用于下一阶段的谓词求值
  • BitWeaving/H
    • 使用了 BitWeaving/V 的对偶形式，列值的所有位都存储在BitWeaving/H格式中
    • 当 fetch整个列时性能很好
    • BitWeaving/H在处理器字之间错开代码，从而产生紧凑的结果位向量，在计算复杂谓词的下一阶段时易于重用

这两个技术都会产生一个 结果向量，每个bit 指明是否与列上的谓词匹配

4 bit的时候，是SIMD scan的 20倍，12bit 是 SMID scan 的4倍
真实场景一般 8 - 16bit，是 SIMD scan 的一个数量级

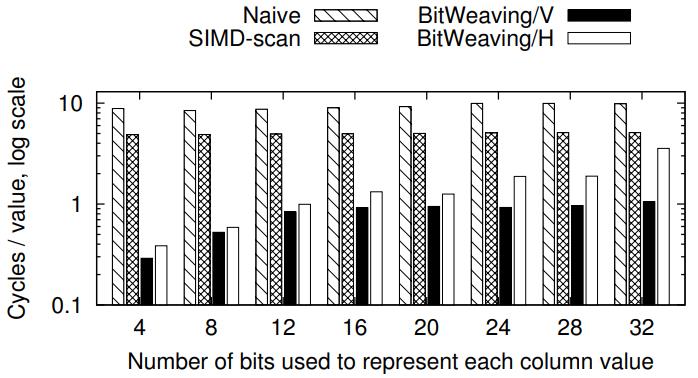
Figure 1: Performance Comparison

BitWeaving 可以作为列存的存储组织格式，也可以作为 行存、列存的索引
相关的压缩操作

  • null suppression
  • prefix suppression
  • frame of reference
  • order-preserving dictionary encoding

这里需要一个 解码操作，才能在之上做 scan

  • 列scan 的输入：n bit 编码code list，以及 基本比较的谓词
  • scan 查找所有满足谓词的 编码code
  • 列scan 的输出：n bit 向量，指明匹配的 code

这里使用一个 处理器字，一般就是 64bit 的宽度，借助 SIMD，可以扩展到更宽的维度
假设 宽度为w
k是需要编码一个列 C 的需要的 bit 数量
n是 codes数量
并行度为 $\frac{kn}{w}$

并行scan的计算方式

  • 基于单表的复杂谓词求值
  • 包含各种 AND、OR，以及各种比较操作
  • 评估算法会产出一个 bit 向量，如果列值被选中了，则对应的 bit 就被设置
  • 产出后的结果，可以用于后续继续求值计算
  • 谓词求值是按照 binary tree形式计算的，叶节点封装基本比较操作，AND、OR、NOT作为中间节点
  • 用 DFS 遍历谓词树，在每个叶节点上执行比较，在中间节点做合并

实现细节

HBP 和 VBP 是 两种表示方式

  • HBP 相当于是面向行级别的 bit 存储
  • VBP 相当于是列级别的 bit 存储
  • 优化目标是，减少指令数量，以及底层数据的cache line存储
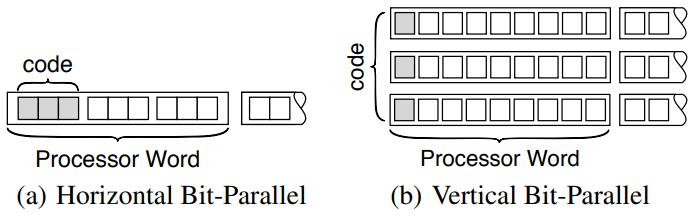
    Figure 2: HBP and VBP layouts for a column with 3-bit codes. The shaded boxes represent the bits for the first column value.

HBP

HBP 将一个 code打包到处理器字中，基于普通的全字指令，实现硬件实现的 SIM 指令功能
HBP 可以解决的问题：列的宽度通常与 SIMD 处理器宽度不匹配，导致并行性无法充分利用
HBP 将 k + 1 个 bit打包到一个处理器字中，其中 k 是编码长度，阴影部分是 1bit，用于做分隔符的
这里按照一定的规则进行分段处理，下图是 8 个 code 分为一个 segment

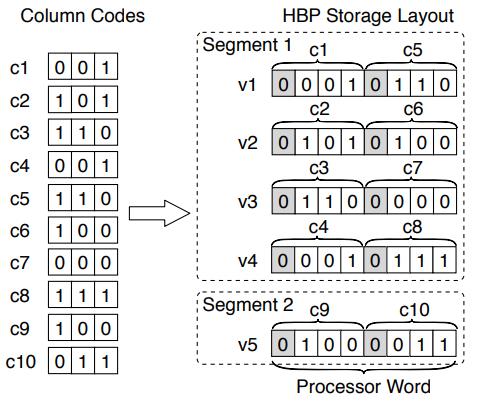
Figure 3: Example of the HBP storage layout (k = 3, w = 8). Delimiter bits are marked in gray.

计算 X op Y 的操作，X 被打包到寄存器中了，所以无法直接处理，需要跟 Y 做 bit运算
这里 Xi 就是一组code 值，每个Yi 都是一个谓词常量
经过计算后，如果结果为 $10^k$，也就是 10000…(k个0)，表示 true
如果是 $0^k+1$，k+1个0，就表示 false

然后就是几个 比较操作
相等、不等、>、>=，其他 <，<= 只需要swap 两边就可以了
如果 x != y，那么 x 亦或^ y 不等于 0000(k+1个0)
因此 ((x ^ y) + $01^k$ ) & $10^k$ = $10^k$，判断最左边的 分割标志位是否为 1，就知道结果了
用类似的方式就可以计算出 相等、小于、小于等于了

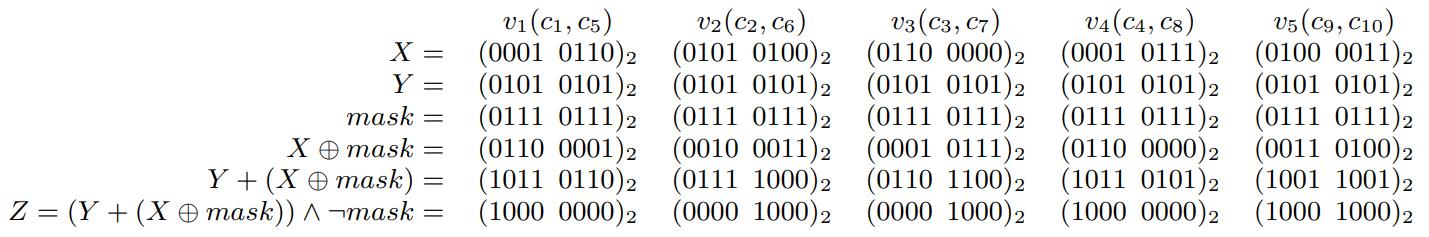
Figure 4: Evaluating a predicate c < 5 on the example column c

按照图3 的显示方式，c1、c2、c3、c4的结果需要做合并
c1的最左边不懂，c2右移1位，c3移动2位，c4移动3位
然后 c1 OR c2 OR c3 OR c4，就能得到结果了
c5 - c8 也是同样的方式，这也就解释了为什么 HBP 使用这种方式布局了

VBP

VBP 的存储方式相当于 列级别的 bit 存储
左边有 10个 code，分为两个 segment
code 的第一个 bit 存储到 VBP 的 v1中，第二个bit 存储到 v2中，以此类推
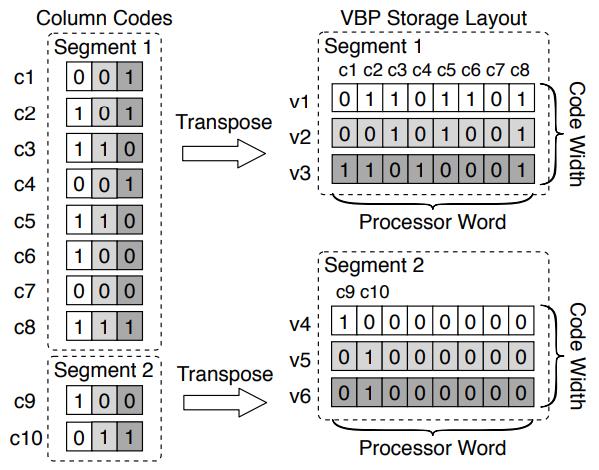Figure 5: Example of the VBP storage layout. The middle bits of codes are marked in light gray, whereas the least significant bits are marked in dark gray

VBP 的比较方式

  • 先构建垂直的 C1、C2，然后垂直的从最左开始往右遍历
  • 计算出 gt、lt，不断遍历直到结束
  • 最后通过 ANT、OR等方式计算 gt 和 lt 的结果，就得到了比较的结果
  • 其他谓词比较方式也是类似的

早期裁剪

适用于 BitWeaving/V
比如 c < 3 这个谓词条件

  • 对于v1，它存储了 第一列bit，因此v1中所有 包含 1 的 bit 为都不符合条件，为 3 是011，第一位是 1就变成大于了
  • v1过滤后，就是c1、c4、c6满足条件，再比较v2
  • 此时这三个都是0，所以前两位是 00，小于3 的前两位 01
  • 因此就可以终止计算了，c1、c4、c6 满足条件 Figure 6: Evaluating c < 3 with the early pruning technique

早期裁剪的概率，有些 segment没有填充满，比如 segment2
在 bit位较少的时候，裁剪概率都很低，而随着bit 位增加，裁剪概率都趋向于 1
比如 10%充填率情况下，8个bit 的裁剪概率为 97.5%
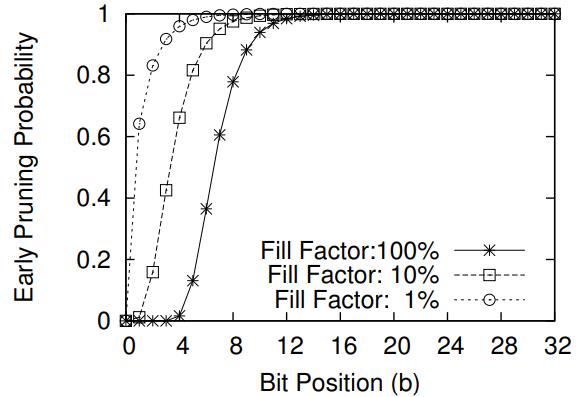Figure 7: Early Pruning Probability P(b)

对于复杂的谓词，早期裁剪可以传递
比如 R.a < 10，这个早期裁剪的结果，可以作为 R.b > 5的候选条件
同样 R.b > 5 再次过滤后，可以作为 R.c < 20 的候选条件
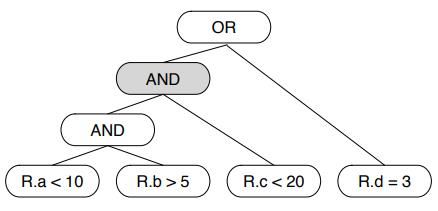Figure 8: An example predicate tree for the expression
R.a < 10 AND R.b > 5 AND R.c < 20 OR R.d = 3

Bit Weaving

HBP 和 VBP 的统称
VBP的优势

  • 可以运行早期裁剪，减少scan bit 的数量
  • 存储格式不是纯的 VBP格式，但是水平打包后分组后，可以进一步利用早期裁剪
  • 可以利用 SIMD 指令

对于普通的 VBP 这里有一个布局优化
假设 9一个 processor word 一组，也就是一个 segment，通过裁剪，可以跳过后面 6个
而这 6而需要加载到 cache line 中，这样就浪费了内存带宽
于是将 9个 word 水平拆分成 3个 big group
这样 cut-off 的时候，只需要读 bit group 1 的第一组和 bit group 2 的第一组
减少了内存带宽浪费
当然，设置 3只是一个理论值，如果 是 2个bit skip，仍然会有一些浪费
如何精准的设置多少 processor word为一组，也是一个开放话题
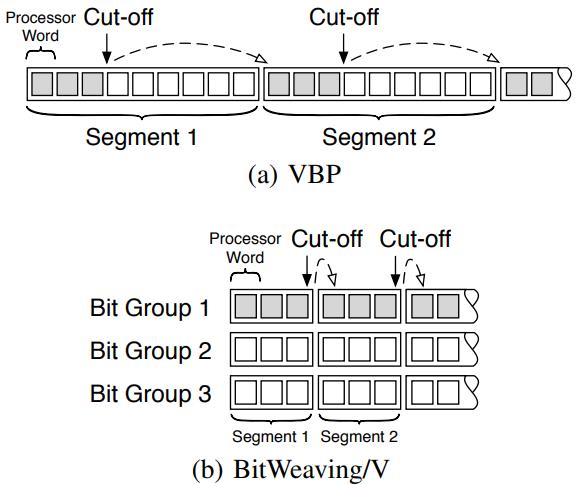Figure 9: Early pruning on VBP and BitWeaving/V

比较一下 BitWeaving/H 和 BitWeaving/V

  • scan复杂度上，两者差不多，H 方式会多一个分隔符位置，多一个bit
  • SIMD，H方式也可以使用SIMD但需要填充，可能无法充分利用，V 的方式可以充分利用带宽
  • 早期裁剪，H 方式不支持，V 的方式支持
  • 查找性能，H的方式方便查询，但 V 是将 code跨多个处理器word分布了，会损失性能 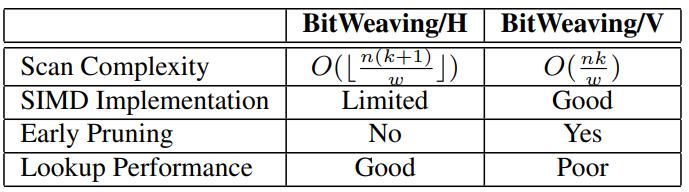Table 1: Comparing BitWeaving/H and BitWeaving/V

性能评估

对比 native、SIMD、Bit-sliced、BL、BitWeaving/V、BitWeaving/H

  • 原生的是最差的
  • SIMD 有了很大提升，但是因为打包对其占用了额外开销导致性能不加
  • Bit-sliced 效果也不错
  • 最好的是 BitWeaving，对于cache miss和指令数量都做了优化
  • Q1查询： SELECT COUNT(*) FROM R WHERE R.a < C1
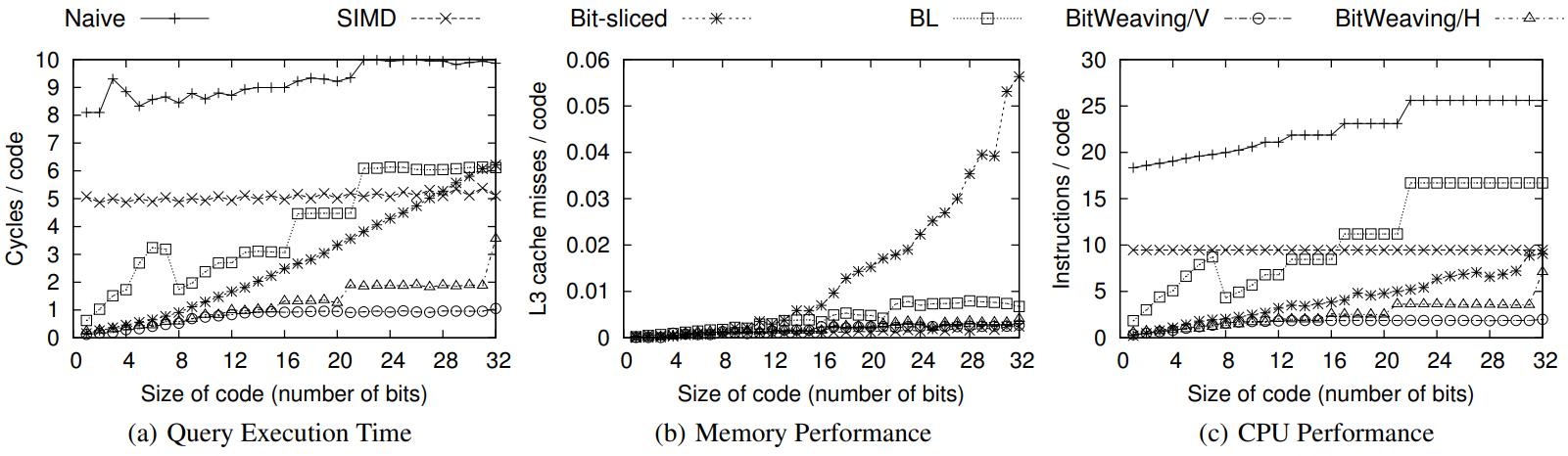    Figure 10: Performance on query Q1.

对比 HBP、VBP

  • 可以看到 VPB + SIMD，以及 VBP + 早期裁剪之后，比原生的 VBP要快很多
  • HBP 也可以加上 SIMD，早期裁剪，但是会带来很多性能损失，结果性能反而下降
  • 查询性能看，HBP表现的很稳定，而 VBP需要跨 processor word，有cache miss，性能会下降很多 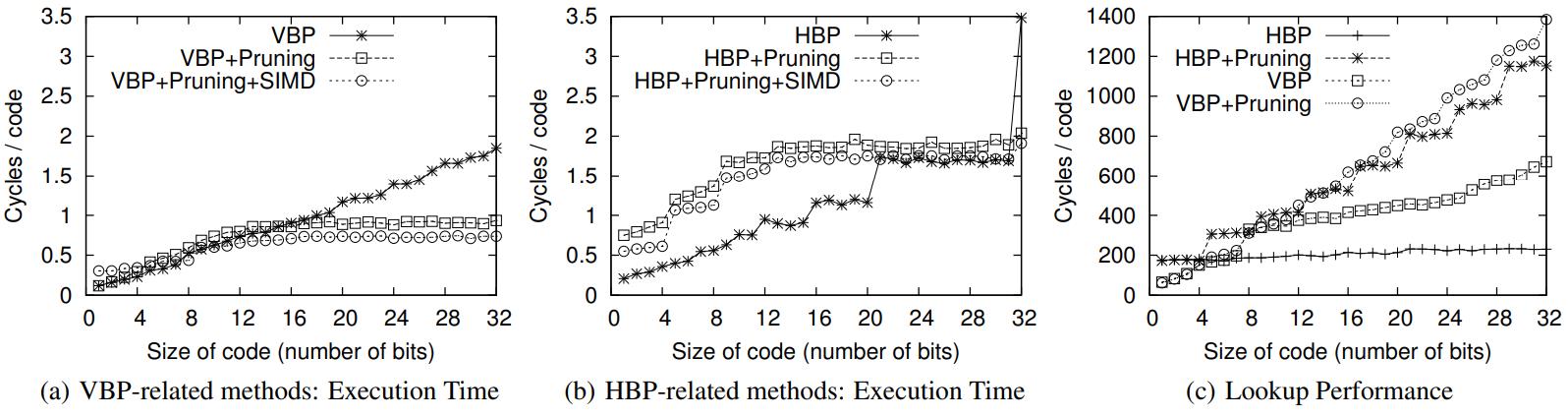Figure 11: Performance comparison between the HBP and the VBP related methods on Query Q1.

下面是执行 TPC-H 的基准测试，数据量为 10G
对于某些查询，因为 BW/V 需要跨多列所以查询性能会下降，BW/H 更好
下图(b)是各种加速对于原生方式的加速比，某些查询 BW可以提高一个数量级
BW/H + 索引效果一般，因为BW/H 本身查询性能就不错
BW/V + 索引能提升一些性能，改进其布局本身的问题
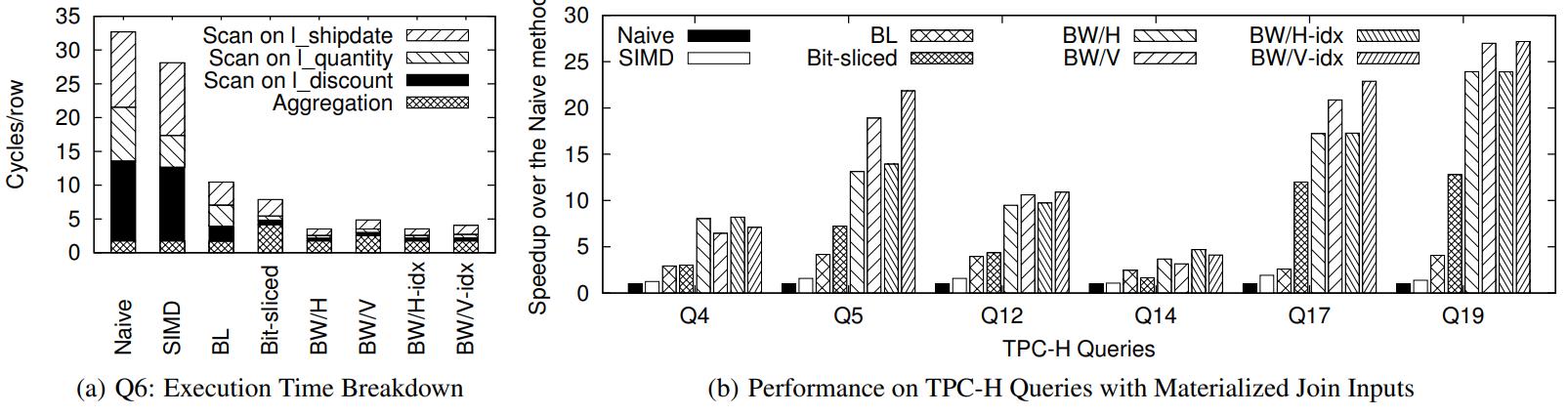Figure 12: Performance comparison with the TPC-H Queries (BW=BitWeaving).

参考